Skip to content

The Hillelogram Verifier Rodeo I (LeftPad)

A month ago, Hillel Wayne posted a verification challenge comprising three problems that might sound frivolous, but which, in fact, hit the sweet spot of being easy to describe and yet interesting to implement and verify. I had a lot of fun hacking them up in LH, and learned some things doing so.

Today, lets see how to implement the first of these challenges -- leftPad -- in Haskell, and to check Hillel's specification with LH.

(Click here to demo)

The LeftPad Challenge

The first of these problems was leftPad

Implementation

First, lets write an idiomatic implementation of leftPad where we will take the liberty of generalizing

  • the padding character to be the input c that is of some (polymorphic) type a
  • the string to be the input xs that is a list of a

If the target length n is indeed greater than the input string xs, i.e. if k = n - size xs is positive, we replicate the character c k times and append the result to the left of the input xs. Otherwise, if k is negative, we do nothing, i.e. return the input.

87: {-@ reflect leftPad @-}
88: leftPad :: Int -> a -> [a] -> [a]
89: x1:GHC.Types.Int -> a -> x3:[a] -> {res : [a] | size res == max x1 (size x3)}leftPad GHC.Types.Intn ac [a]xs
90:   | GHC.Types.Bool0 x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Bool | v <=> x1 < x2}< k     = {v : x1:a -> {v : [a] | size v == k
                        && v == replicate k x1
                        && v == (if 0 == k then [] else : x1 (replicate (k - 1) x1))} | v == replicate k}replicate k c ++ xs
91:   | otherwise = xs
92:   where
93:     GHC.Types.Intk         = GHC.Types.Intn x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- {v : GHC.Types.Int | v >= 0
                     && v == size xs}size xs

The code for leftPad is short because we've delegated much of the work to size, replicate and ++. Here's how we can compute the size of a list:

101: {-@ measure size @-}
102: {-@ size :: [a] -> Nat @-}
103: x1:[a] -> {v : GHC.Types.Int | v >= 0
                               && v == size x1}size []     = 0
104: size (x:xs) = {v : GHC.Types.Int | v == (1 : int)}1 x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 + x2}+ {v : GHC.Types.Int | v >= 0
                     && v == size xs}size xs

and here is the list append function ++ :

110: {-@ reflect ++ @-}
111: {-@ (++) :: xs:[a] -> ys:[a] ->
112:             {v:[a] | size v = size xs + size ys}
113:   @-}
114: []     x1:[a] -> x2:[a] -> {v : [a] | size v == size x1 + size x2}++ [a]ys = ys
115: (x:xs) ++ ys = x : ({v : [a] | size v == size xs + size ys
           && v == ++ xs ys}xs ++ ys)

and finally the implementation of replicate :

121: {-@ reflect replicate @-}
122: {-@ replicate :: n:Nat -> a ->
123:                  {v:[a] | size v = n}
124:   @-}
125: x1:{v : GHC.Types.Int | v >= 0} -> a -> {v : [a] | size v == x1}replicate 0 _ = []
126: replicate n c = c : x1:{v : GHC.Types.Int | v >= 0} -> a -> {v : [a] | size v == x1}replicate (GHC.Types.Intn x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- 1) c

What shall we Prove?

My eyes roll whenever I read the phrase "proved X (a function, a program) correct".

There is no such thing as "correct".

There are only "specifications" or "properties", and proofs that ensures that your code matches those specifications or properties.

What specifications shall we verify about our implementation of leftPad? One might argue that the above code is "obviously correct", i.e. the implementation more or less directly matches the informal requirements.

One way to formalize this notion of "obviously correct" is to verify a specification that directly captures the informal requirements:

151: {-@ obviously :: n:Int -> c:a -> xs:[a] ->
152:       { leftPad n c xs = if (size xs < n)
                         then (replicate (n - size xs) c ++ xs)
                         else xs }
155:   @-}
156: x1:GHC.Types.Int -> x2:a -> x3:[a] -> {VV : () | leftPad x1 x2 x3 == (if size x3 < x1 then ++ (replicate (x1 - size x3) x2) x3 else x3)}obviously _ _ _ = ()

In the above, the type signature is a specification that says that for all n, c and xs, the value returned by leftPad n c xs is xs when n is too small, and the suitably padded definition otherwise.

The code, namely (), is the proof. LH is able to trivially check that leftPad meets the "obviously correct" specification, because, well, in this case, the implementation is the specification. (Incidentally, this is also why the Idris solution is terse.)

So, if you are happy with the above specification, you can stop reading right here: we're done.

Hillel's Specifications

However, the verification rodeo is made more interesting by Hillel's Dafny specifications:

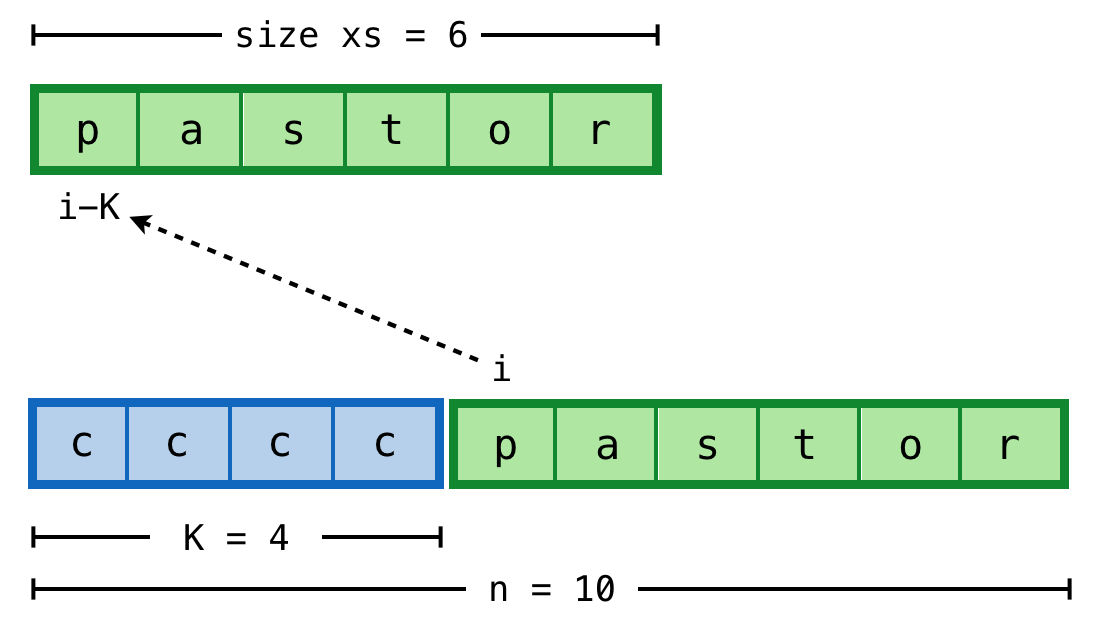
  1. Size The size of the returned sequence is the larger of n and the size of xs;

  2. Pad-Value Let K = n - size xs. We require that the i-th element of the padded-sequence is c if 0 <= i < K, and is the i - K-th element of xs otherwise.

Ribbons

Digression: The Importance of being Decidable

LH, like many of the other rodeo entries, uses SMT solvers to automate verification. For example, the leftPad solutions in Dafny and SPARK and F* make heavy use quantified axioms to encode properties of sequences.

However, unlike its many SMT-based brethren, LH takes a somewhat fanatical stance: it never uses quantifiers or axioms. We take this rigid position because SMT solvers are only predictable on queries from (certain) decidable logics. Axioms, or more generally, quantified formulas rapidly take SMT solvers out of this "comfort zone", causing them to reject valid formulas, run slowly, or even, to run forever.

Thus, we have chosen to deliberately avoid the siren song of quantifiers by lashing LH firmly to the steady mast of decidable logics.

Reasoning about Sequences

Unfortunately, this design choice leaves us with some work: we must develop i.e. state and prove relevant properties about sequences from scratch.

Indexing into a Sequence

To start, lets define the notion of the i-th element of a sequence (this is pretty much Haskell's list-index operator)

247: {-@ reflect !! @-}
248: {-@ (!!) :: xs:[a] -> {n:Nat | n < size xs} -> a @-}
249: (x:_)  x1:[a] -> {v : GHC.Types.Int | v >= 0
                               && v < size x1} -> a!! 0 = x
250: (_:xs) !! n = x1:[a] -> {v : GHC.Types.Int | v >= 0
                               && v < size x1} -> axs !! (GHC.Types.Intn x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- 1)

Replicated Sequences

Next, we verify that every element in a replicate-d sequence is the element being cloned:

259: {-@ thmReplicate :: n:Nat -> c:a -> i:{Nat | i < n} ->
260:                     { replicate n c !! i  == c }
261:   @-}
262: x1:{v : GHC.Types.Int | v >= 0} -> x2:a -> x3:{v : GHC.Types.Int | v >= 0
                                                                   && v < x1} -> {VV : () | !! (replicate x1 x2) x3 == x2}thmReplicate {v : GHC.Types.Int | v >= 0}n ac {v : GHC.Types.Int | v >= 0
                     && v < n}i
263:   | GHC.Types.Booli x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Bool | v <=> x1 == x2}== 0    = ()
264:   | otherwise = x1:{v : GHC.Types.Int | v >= 0} -> x2:a -> x3:{v : GHC.Types.Int | v >= 0
                                                                   && v < x1} -> {VV : () | !! (replicate x1 x2) x3 == x2}thmReplicate (GHC.Types.Intn x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- 1) c (GHC.Types.Inti x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- 1)

LH verifies the above "proof by induction":

  • In the base case i == 0 and the value returned is c by the definition of replicate and !!.

  • In the inductive case, replicate n c !! i is equal to replicate (n-1) c !! (i-1) which, by the "induction hypothesis" (i.e. by recursively calling the theorem) is c.

Concatenating Sequences

Finally, we need two properties that relate concatenation and appending, namely, the i-th element of xs ++ ys is:

  • Left the i-th element of xs if 0 <= i < size xs, and
  • Right the i - size xs element of ys otherwise.
286: {-@ thmAppLeft :: xs:[a] -> ys:[a] -> {i:Nat | i < size xs} ->
287:                   { (xs ++ ys) !! i == xs !! i }
288:   @-}
289: x1:[a] -> x2:[a] -> x3:{v : GHC.Types.Int | v >= 0
                                            && v < size x1} -> {VV : () | !! (++ x1 x2) x3 == !! x1 x3}thmAppLeft (x:xs) [a]ys 0 = ()
290: thmAppLeft (x:xs) ys i = x1:[a] -> x2:[a] -> x3:{v : GHC.Types.Int | v >= 0
                                            && v < size x1} -> {VV : () | !! (++ x1 x2) x3 == !! x1 x3}thmAppLeft xs ys (GHC.Types.Intix1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}-1)
291: 
292: {-@ thmAppRight :: xs:[a] -> ys:[a] -> {i:Nat | size xs <= i} ->
293:                    { (xs ++ ys) !! i == ys !! (i - size xs) }
294:   @-}
295: x1:[a] -> x2:[a] -> x3:{v : GHC.Types.Int | v >= 0
                                            && size x1 <= v} -> {VV : () | !! (++ x1 x2) x3 == !! x2 (x3 - size x1)}thmAppRight []     [a]ys {v : GHC.Types.Int | v >= 0}i = ()
296: thmAppRight (x:xs) ys i = x1:[a] -> x2:[a] -> x3:{v : GHC.Types.Int | v >= 0
                                            && size x1 <= v} -> {VV : () | !! (++ x1 x2) x3 == !! x2 (x3 - size x1)}thmAppRight xs ys (GHC.Types.Intix1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}-1)

Both of the above properties are proved by induction on i.

Proving Hillel's Specifications

Finally, we're ready to state and prove Hillel's specifications.

Size Specification

The size specification is straightforward, in that LH proves it automatically, when type-checking leftPad against the signature:

313: {-@ leftPad :: n:Int -> c:a -> xs:[a] ->
314:                 {res:[a] | size res = max n (size xs)}
315:   @-}

Pad-Value Specification

We specify the pad-value property -- i.e. the i-th element equals c or the corresponding element of xs -- by a type signature:

325: {-@ thmLeftPad
326:       :: n:_ -> c:_ -> xs:{size xs < n} -> i:{Nat | i < n} ->
327:          { leftPad n c xs !! i ==  leftPadVal n c xs i }
328:   @-}
329: 
330: {-@ reflect leftPadVal @-}
331: {n : GHC.Types.Int | False} -> a -> [a] -> GHC.Types.Int -> aleftPadVal {n : GHC.Types.Int | False}n ac [a]xs GHC.Types.Inti
332:   | {v : GHC.Types.Bool | v <=> i < k}i x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Bool | v <=> x1 < x2}< k     = c
333:   | otherwise = {v : [a] | size v >= 0
           && len v >= 0
           && v == xs}xs !! ({v : GHC.Types.Int | v == i - k}i x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- k)
334:   where GHC.Types.Intk     = {v : GHC.Types.Int | v >= 0
                     && v == size xs}n x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- size xs

Pad-Value Verification

We verify the above property by filling in the implementation of thmLeftPad as:

343: x1:GHC.Types.Int -> x2:a -> x3:{v : [a] | size v < x1} -> x4:{v : GHC.Types.Int | v >= 0
                                                                                  && v < x1} -> {VV : () | !! (leftPad x1 x2 x3) x4 == leftPadVal x1 x2 x3 x4}thmLeftPad GHC.Types.Intn ac {v : [a] | size v < n}xs {v : GHC.Types.Int | v >= 0
                     && v < n}i
344:   | {v : GHC.Types.Bool | v <=> i < k}i x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Bool | v <=> x1 < x2}< k     = x1:[a] -> x2:{v : GHC.Types.Int | v >= 0
                                  && v < size cs} -> {v : () | !! (++ cs x1) x2 == !! cs x2}thmAppLeft  cs xs i `seq` x1:a -> x2:{v : GHC.Types.Int | v >= 0
                                && v < k} -> {v : () | !! (replicate k x1) x2 == x1}thmReplicate k c i
345:   | otherwise = x1:[a] -> x2:{v : GHC.Types.Int | v >= 0
                                  && size cs <= v} -> {v : () | !! (++ cs x1) x2 == !! x1 (x2 - size cs)}thmAppRight cs xs i
346:   where
347:     GHC.Types.Intk         = GHC.Types.Intn x1:GHC.Types.Int -> x2:GHC.Types.Int -> {v : GHC.Types.Int | v == x1 - x2}- {v : GHC.Types.Int | v >= 0
                     && v == size xs}size xs
348:     {v : [a] | size v == k
           && v == replicate k c
           && v == (if 0 == k then [] else : c (replicate (k - 1) c))}cs        = {v : x1:a -> {v : [a] | size v == k
                        && v == replicate k x1
                        && v == (if 0 == k then [] else : x1 (replicate (k - 1) x1))} | v == replicate k}replicate k c

The "proof" -- in quotes because its just a Haskell function -- simply combines the replicate- and concatenate-left theorems if i is in the "pad", and the concatenate-right theorem, otherwise.

Conclusions

That concludes part I of the rodeo. What did I learn from this exercise?

  1. Even apparently simple functions like leftPad can have many different specifications; there is no necessarily "best" specification as different specs make different assumptions about what is "trusted", and more importantly, though we didn't see it here, ultimately a spec is a particular view into how a piece of code behaves and we may want different views depending on the context where we want to use the given piece of code.

  2. The leftPad exercise illustrates a fundamental problem with Floyd-Hoare style "modular" verification, where pre- and post-conditions (or contracts or refinement types or ...) are used to modularly "abstract" functions i.e. are used to describe the behavior of a function at a call-site. As the above exercise shows, we often need properties connecting the behavior of different functions, e.g. append (++), indexing (!!). In these cases, the only meaningful specification for the underlying function is its implementation.

  3. Finally, the above proofs are all over user-defined recursive functions which this was not even possible before refinement reflection, i.e till about a year ago. I'm also quite pleased by how logical evaluation makes these proofs quite short, letting LH verify expressive specifications while steering clear of the siren song of quantifiers.

Ranjit Jhala
2018-05-17
reflection