Arithmetic Overflows
Computers are great at crunching numbers. However, if programmers aren't careful, their machines can end up biting off more than they can chew: simple arithmetic operations over very large (or very tiny) inputs can overflow leading to bizarre crashes or vulnerabilities. For example, Joshua Bloch's classic post argues that nearly all binary searches are broken due to integer overflows. Lets see how we can teach LiquidHaskell to spot such overflows.
30: module Bounded where 31: 32: import Control.Exception (assert) 33: import Prelude hiding (Num (..)) 34: import qualified Prelude 35: 36: plusStrict :: Int -> Int -> Int 37: plusLazy :: Int -> Int -> Int 38: mono :: Int -> Bool
1. The Problem¶
LiquidHaskell, like some programmers, likes to make believe
that Int represents the set of integers. For example, you
might define a function plus as:
51: {-@ plus :: x:Int -> y:Int -> {v:Int | v == x + y} @-} 52: plus :: Int -> Int -> Int 53: x1:Int -> x2:Int -> {v : Int | v == x1 + x2}plus Intx Inty = {v : Int | v == y}x x1:Int -> x2:Int -> {v : Int | v == x1 + x2}Prelude.+ y
The output type of the function states that the returned value is equal to the \emph{logical} result of adding the two inputs.
The above signature lets us "prove" facts like addition by one yields a bigger number:
63: {-@ monoPlus :: Int -> {v:Bool | v <=> true } @-} 64: monoPlus :: Int -> Bool 65: Int -> {v : Bool | v <=> true}monoPlus Intx = {v : Int | v == x}x x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< {v : x1:Int -> x2:Int -> {v : Int | v == x1 + x2} | v == Bounded.plus}plus x 1
Unfortunately, the signature for plus and hence, the above "fact" are both lies.
LH checks plus as the same signature is assumed
for the primitive Int addition operator Prelude.+.
LH has to assume some signature for this "foreign"
machine operation, and by default, LH assumes that
machine addition behaves like logical addition.
However, this assumption, and its consequences are only true upto a point:
λ> monoPlus 0
True
λ> monoPlus 100
True
λ> monoPlus 10000
True
λ> monoPlus 1000000
True
Once we get to maxBound at the very edge of Int,
a tiny bump is enough to send us tumbling backwards
into a twilight zone.
λ> monoPlus maxBound
False
λ> plus maxBound 1
-9223372036854775808
2. Keeping Int In Their Place¶
The news isn't all bad: the glass half full
view is that for "reasonable" values
like 10, 100, 10000 and 1000000, the
machine's arithmetic is the same as
logical arithmetic. Lets see how to impart
this wisdom to LH. We do this in two steps:
define the biggest Int value, and then,
use this value to type the arithmetic operations.
A. The Biggest Int
First, we need a way to talk about
"the edge" -- i.e. the largest Int
value at which overflows occur.
We could use the concrete number
λ> maxBound :: Int
9223372036854775807
However, instead of hardwiring a particular number,
a more general strategy is to define a symbolic
constant maxInt to represent any arbitrary
overflow value and thus, make the type checking
robust to different machine integer widths.
135: -- defines an Int constant called `maxInt` 136: {-@ measure maxInt :: Int @-}
To tell LH that maxInt is the "biggest" Int,
we write a predicate that describes values bounded
by maxInt:
144: {-@ predicate Bounded N = 0 < N + maxInt && N < maxInt @-}
Thus, Bounded n means that the number n is in
the range [-maxInt, maxInt].
B. Bounded Machine Arithmetic
Next, we can assign the machine arithmetic operations types that properly capture the possibility of arithmetic overflows. Here are two possible specifications.
Strict: Thou Shalt Not Overflow A strict specification simply prohibits any overflow:
160: {-@ plusStrict :: x:Int -> y:{Int|Bounded(x+y)} -> {v:Int|v = x+y} @-} 161: x1:Int -> x2:{y : Int | 0 < (x1 + y) + maxInt && x1 + y < maxInt} -> {v : Int | v == x1 + x2}plusStrict Intx {y : Int | 0 < (x + y) + maxInt && x + y < maxInt}y = {v : Int | 0 < (x + v) + maxInt && x + v < maxInt && v == y}x x1:Int -> x2:Int -> {v : Int | v == x1 + x2}Prelude.+ y
The inputs x and y must be such that the result is Bounded,
and in that case, the output value is indeed their logical sum.
Lazy: Overflow at Thine Own Risk Instead, a lazy specification could permit overflows but gives no guarantees about the output when they occur.
172: {-@ plusLazy :: x:Int -> y:Int -> {v:Int|Bounded(x+y) => v = x+y} @-} 173: x1:Int -> x2:Int -> {v : Int | 0 < (x1 + x2) + maxInt && x1 + x2 < maxInt => v == x1 + x2}plusLazy Intx Inty = {v : Int | v == y}x x1:Int -> x2:Int -> {v : Int | v == x1 + x2}Prelude.+ y
The lazy specification says that while plusLazy
can be called with any values you like, the
result is the logical sum
only if there is no overflow.
To understand the difference between the two
specifications, lets revisit the monoPlus
property using the new machine-arithmetic
sensitive signatures:
188: {-@ monoPlusStrict :: Int -> {v:Bool | v <=> true } @-} 189: Int -> {v : Bool | v <=> true}monoPlusStrict Intx = {v : Int | v == x}x x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< {v : x1:Int -> x2:{v : Int | 0 < (x1 + v) + maxInt && x1 + v < maxInt} -> {v : Int | v == x1 + x2} | v == Bounded.plusStrict}plusStrict x 1 190: 191: {-@ monoPlusLazy :: Int -> {v:Bool | v <=> true } @-} 192: Int -> {v : Bool | v <=> true}monoPlusLazy Intx = {v : Int | v == x}x x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< {v : x1:Int -> x2:Int -> {v : Int | 0 < (x1 + x2) + maxInt && x1 + x2 < maxInt => v == x1 + x2} | v == Bounded.plusLazy}plusLazy x 1
Both are rejected by LH, since, as we saw earlier,
the functions do not always evaluate to True.
However, in the strict version the error is at the
possibly overflowing call to plusStrict.
In the lazy version, the call to plusLazy is
accepted, but as the returned value is some
arbitrary Int (not the logical x+1), the
comparison may return False hence the output
is not always True.
Exercise: Can you fix the specification
for monoPlusStrict and monoPlusLazy to
get LH to verify the implementation?
3. A Typeclass for Machine Arithmetic¶
Its a bit inconvenient to write plusStrict and plusLazy,
and really, we'd just like to write + and - and so on.
We can do so, by tucking the above specifications into
a bounded numeric typeclass whose signatures capture machine
arithmetic. First, we define a BoundedNum variant of Num
220: class BoundedNum a where 221: (+) :: a -> a -> a 222: (-) :: a -> a -> a 223: -- other operations ...
and now, we can define its Int instance just as wrappers
around the Prelude operations:
230: instance BoundedNum Int where 231: Intx x1:Int -> x2:{y : Int | 0 < (x1 + y) + maxInt && x1 + y < maxInt} -> {v : Int | v == x1 + x2}+ {y : Int | 0 < (x + y) + maxInt && x + y < maxInt}y = {v : Int | 0 < (x + v) + maxInt && x + v < maxInt && v == y}x x1:Int -> x2:Int -> {v : Int | v == x1 + x2}Prelude.+ y 232: Intx x1:Int -> x2:{y : Int | 0 < (x1 - y) + maxInt && x1 - y < maxInt} -> {v : Int | v == x1 - x2}- {y : Int | 0 < (x - y) + maxInt && x - y < maxInt}y = {v : Int | 0 < (x - v) + maxInt && x - v < maxInt && v == y}x x1:Int -> x2:Int -> {v : Int | v == x1 - x2}Prelude.- y
Finally, we can tell LH that the above above instance obeys the (strict) specifications for machine arithmetic:
239: {-@ instance BoundedNum Int where 240: + :: x:Int -> y:{Int | Bounded (x+y)} -> {v:Int | v == x+y }; 241: - :: x:Int -> y:{Int | Bounded (x-y)} -> {v:Int | v == x-y } 242: @-}
With the above instance in scope, we can just use the plain +
operator and have LH flag potential overflows:
249: {-@ mono :: Int -> {v:Bool | v <=> true} @-} 250: Int -> {v : Bool | v <=> true}mono Intx = {v : Int | v == x}x x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< Intx + 1
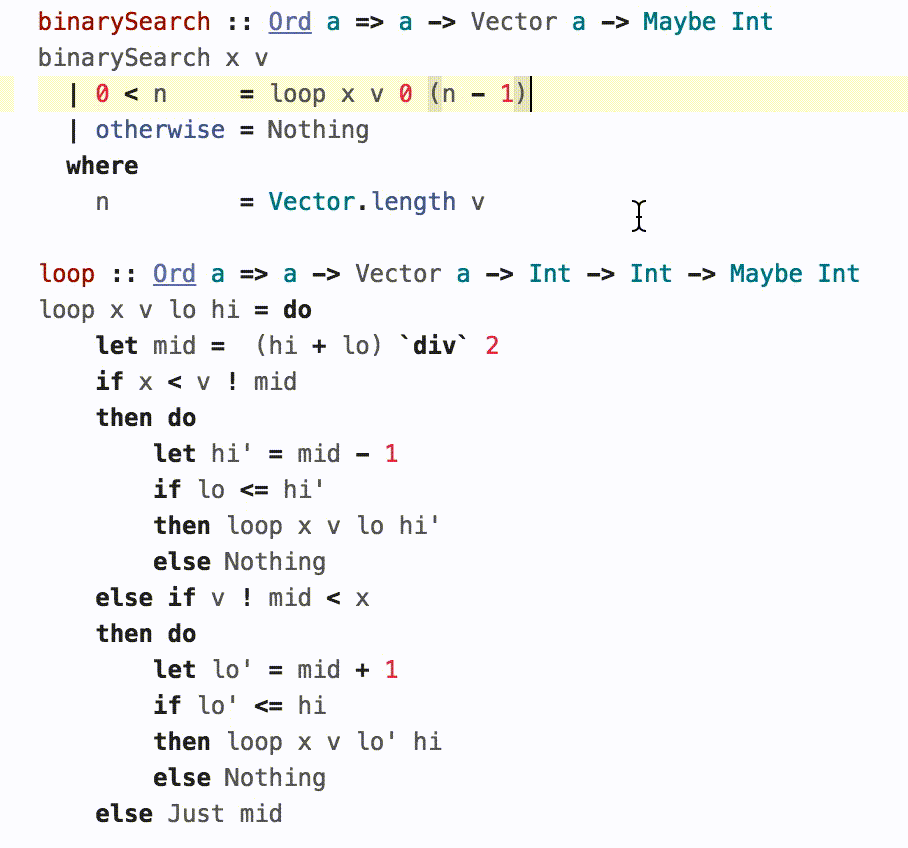
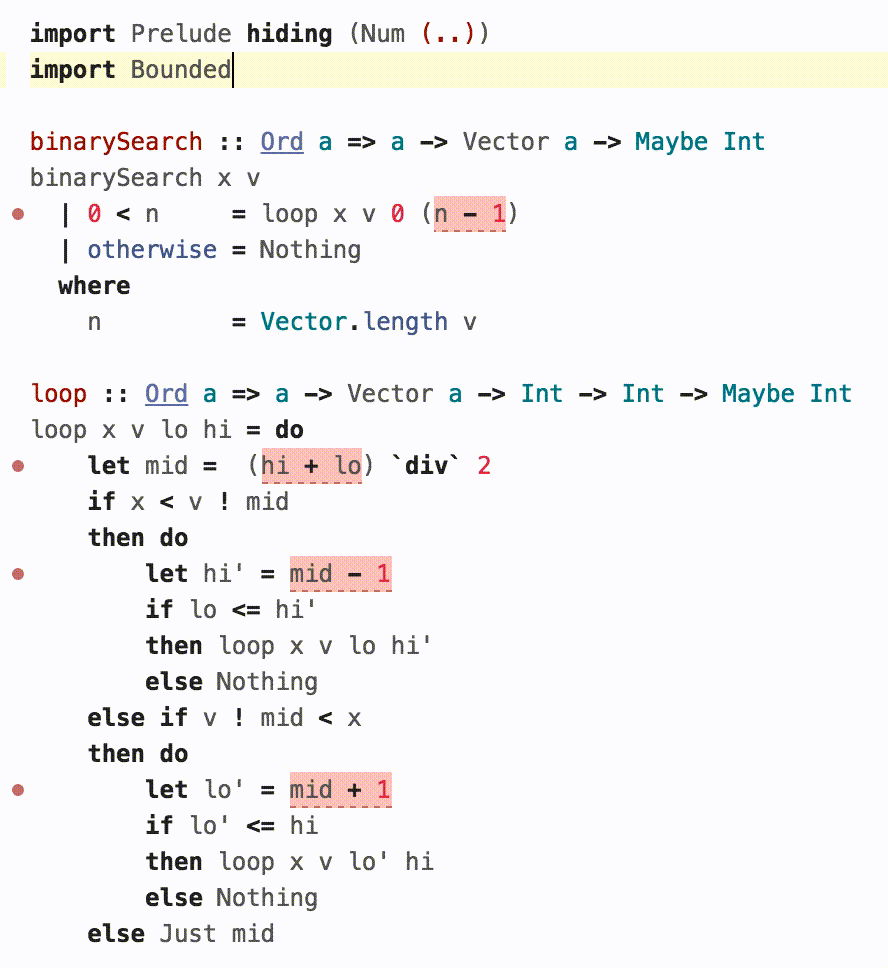
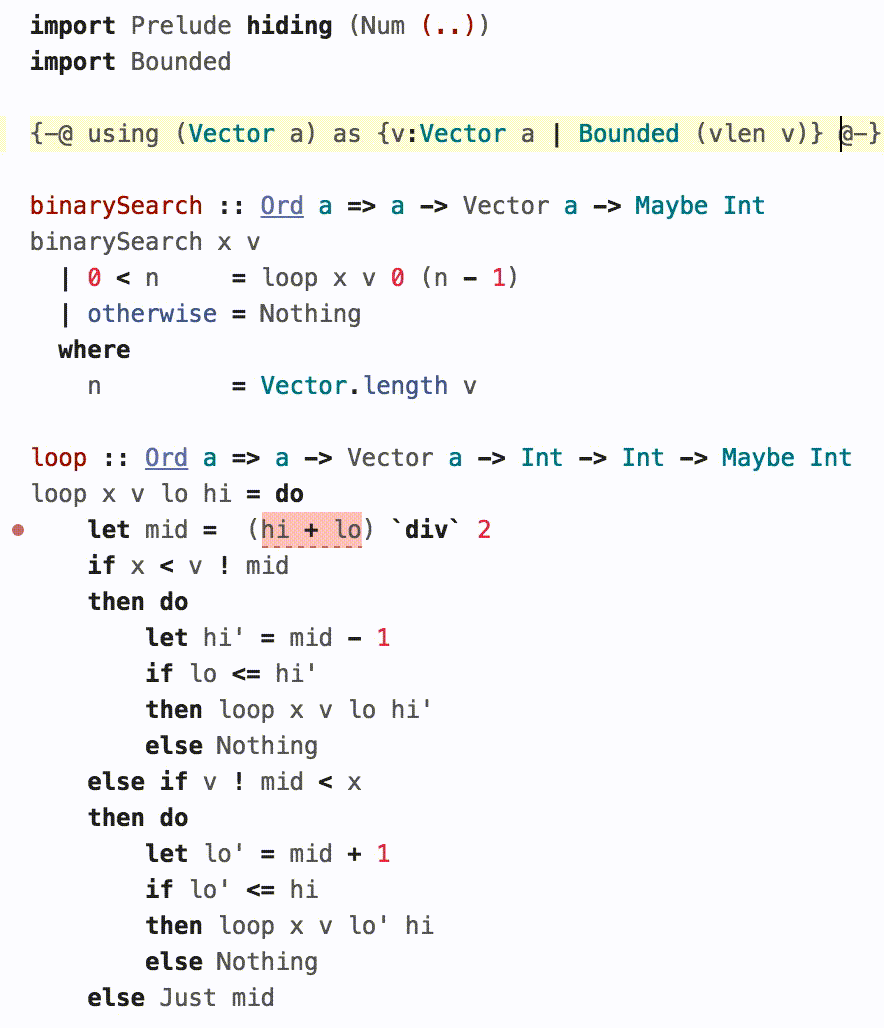
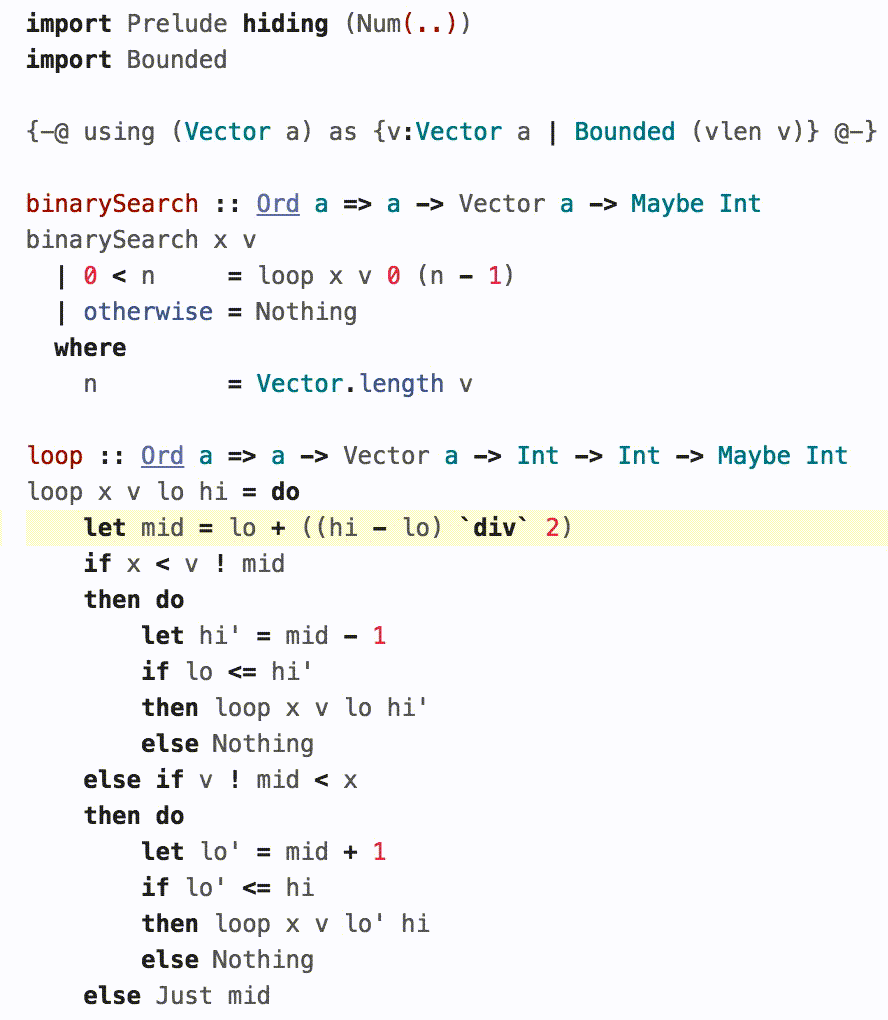
4. An Application: Binary Search¶
The above seems a bit paranoid. Do overflows really matter? And if they do, is it really practical to check for them using the above?
Joshua Bloch's famous article describes a tricky overflow bug in an implementation of binary-search that lay hidden in plain sight in classic textbooks and his own implementation in the JDK for nearly a decade. Gabriel Gonzalez wrote a lovely introduction to LH using binary-search as an example, and a careful reader pointed out that it had the same overflow bug!
Lets see how we might spot and fix such bugs using BoundedNum.
(Hover over the images to animate.)