Refined Datatypes

Sparse Vectors Revisited

As our first example of a refined datatype, let’s revisit the sparse vector representation that we saw earlier. The SparseN type alias we used got the job done, but is not pleasant to work with because we have no way of determining the dimension of the sparse vector. Instead, let’s create a new datatype to represent such vectors:

Thus, a sparse vector is a pair of a dimension and a list of index-value tuples. Implicitly, all indices other than those in the list have the value 0 or the equivalent value type a.

Sparse vectors satisfy two crucial properties. First, the dimension stored in spDim is non-negative. Second, every index in spElems must be valid, i.e. between 0 and the dimension. Unfortunately, Haskell’s type system does not make it easy to ensure that illegal vectors are not representable.¹

Data Invariants LiquidHaskell lets us enforce these invariants with a refined data definition:

Where, as before, we use the aliases:

Refined Data Constructors The refined data definition is internally converted into refined types for the data constructor SP:

-- Generated Internal representation
data Sparse a where
  SP :: spDim:Nat
     -> spElems:[(Btwn 0 spDim, a)]
     -> Sparse a

In other words, by using refined input types for SP we have automatically converted it into a smart constructor that ensures that every instance of a Sparse is legal. Consequently, LiquidHaskell verifies:

but rejects, due to the invalid index:

Field Measures It is convenient to write an alias for sparse vectors of a given size N. We can use the field name spDim as a measure, like vlen. That is, we can use spDim inside refinements²

Let’s write a function to compute a sparse product

LiquidHaskell verifies the above by using the specification to conclude that for each tuple (i, v) in the list y, the value of i is within the bounds of the vector x, thereby proving x ! i safe.

Folded Product We can port the fold-based product to our new representation:

As before, LiquidHaskell checks the above by automatically instantiating refinements for the type parameters of foldl', saving us a fair bit of typing and enabling the use of the elegant polymorphic, higher-order combinators we know and love.

Hint: You need to check that all the indices in elts are less than dim; the easiest way is to compute a new Maybe [(Int, a)] which is Just the original pairs if they are valid, and Nothing otherwise.

Ordered Lists

As a second example of refined data types, let’s consider a different problem: representing ordered sequences. Here’s a type for sequences that mimics the classical list:

The Haskell type above does not state that the elements are in order of course, but we can specify that requirement by refining every element in tl to be greater than hd:

Refined Data Constructors Once again, the refined data definition is internally converted into a “smart” refined data constructor

-- Generated Internal representation
data IncList a where
  Emp  :: IncList a
  (:<) :: hd:a -> tl:IncList {v:a | hd <= v} -> IncList a

which ensures that we can only create legal ordered lists.

It’s all very well to specify ordered lists. Next, lets see how it’s equally easy to establish these invariants by implementing several textbook sorting routines.

First, lets implement insertion sort, which converts an ordinary list [a] into an ordered list IncList a.

The hard work is done by insert which places an element into the correct position of a sorted list. LiquidHaskell infers that if you give insert an element and a sorted list, it returns a sorted list.

Merge Sort Similarly, it is easy to write merge sort, by implementing the three steps. First, we write a function that splits the input into two equal sized halves:

Second, we need a function that combines two ordered lists

Finally, we compose the above steps to divide (i.e. split) and conquer (sort and merge) the input list:

Hint: Think about how append should behave so that the quickSort has the desired property. That is, suppose that ys and zs are already in increasing order. Does that mean that append x ys zs are also in increasing order? No! What other requirement do you need? bottle that intuition into a suitable specification for append and then ensure that the code satisfies that specification.

Ordered Trees

As a last example of refined data types, let us consider binary search ordered trees, defined thus:

enjoy the property that each root lies (strictly) between the elements belonging in the left and right subtrees hanging off the root. The ordering invariant makes it easy to check whether a certain value occurs in the tree. If the tree is empty i.e. a Leaf, then the value does not occur in the tree. If the given value is at the root then the value does occur in the tree. If it is less than (respectively greater than) the root, we recursively check whether the value occurs in the left (respectively right) subtree.

Figure 1.1: A Binary Search Tree with values between 1 and 9. Each root's value lies between the values appearing in its left and right subtrees.

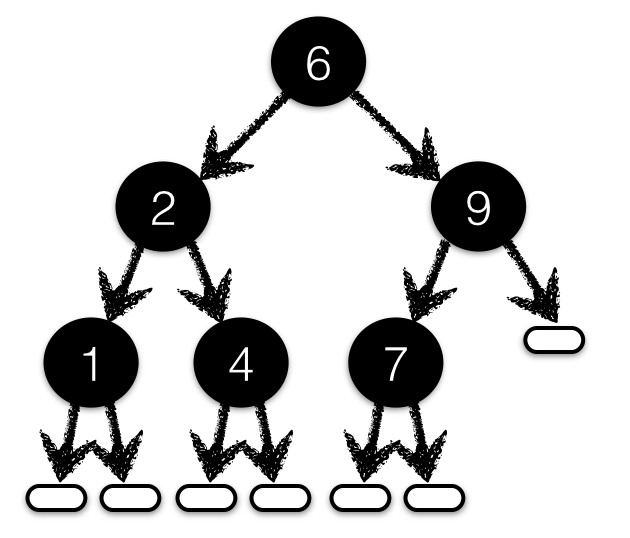
Figure 1.1 shows a binary search tree whose nodes are labeled with a subset of values from 1 to 9. We might represent such a tree with the Haskell value:

Refined Data Type The Haskell type says nothing about the ordering invariant, and hence, cannot prevent us from creating illegal BST values that violate the invariant. We can remedy this with a refined data definition that captures the invariant. The aliases BSTL and BSTR denote BSTs with values less than and greater than some X, respectively.³

Refined Data Constructors As before, the above data definition creates a refined smart constructor for BST

data BST a where
  Leaf :: BST a
  Node :: r:a -> BST {v:a| v < r}
       -> BST {v:a | r < v}
       -> BST a

which prevents us from creating illegal trees

Lets write some functions to create and manipulate these trees. First, a function to check whether a value is in a BST:

Singleton Next, another easy warm-up: a function to create a BST with a single given element:

Insertion Lets write a function that adds an element to a BST.⁴

Minimum For our next trick, lets write a function to delete the minimum element from a BST. This function will return a pair of outputs – the smallest element and the remainder of the tree. We can say that the output element is indeed the smallest, by saying that the remainder’s elements exceed the element. To this end, lets define a helper type: ⁵

We can specify that mElt is indeed smaller than all the elements in rest via the data type refinement:

Finally, we can write the code to compute MinPair

Hint: This exercise will be a lot easier after you finish the quickSort exercise. Note that the signature for toIncList does not use Ord and so you cannot (and need not) use a sorting procedure to implement it.

Recap

In this chapter we saw how LiquidHaskell lets you refine data type definitions to capture sophisticated invariants. These definitions are internally represented by refining the types of the data constructors, automatically making them “smart” in that they preclude the creation of illegal values that violate the invariants. We will see much more of this handy technique in future chapters.

One recurring theme in this chapter was that we had to create new versions of standard datatypes, just in order to specify certain invariants. For example, we had to write a special list type, with its own copies of nil and cons. Similarly, to implement delMin we had to create our own pair type.

This duplication of types is quite tedious. There should be a way to just slap the desired invariants on to existing types, thereby facilitating their reuse. In a few chapters, we will see how to achieve this reuse by abstracting refinements from the definitions of datatypes or functions in the same way we abstract the element type a from containers like [a] or BST a.