Previously, we saw how the principle of “making illegal states unrepresentable” allowed LH to easily enforce a key invariant in Joachim Breitner’s library for representing sets of integers as sorted lists of intervals.
However, Hs-to-coq let Breitner specify and verify that his code properly implemented a set library. Today, lets see how LH’s new “type-level computation” abilities let us reason about the sets of values corresponding to intervals, while using the SMT solver to greatly simplify the overhead of proof.
(Click here to demo)

42: {-@ LIQUID "--short-names" @-} 43: {-@ LIQUID "--exact-data-con" @-} 44: {-@ LIQUID "--no-adt" @-} 45: {-@ LIQUID "--higherorder" @-} 46: {-@ LIQUID "--diff" @-} 47: {-@ LIQUID "--ple" @-} 48: 49: module RangeSet where 50: 51: import Prelude hiding (min, max) 52: import Language.Haskell.Liquid.NewProofCombinators
Intervals
Recall that the key idea is to represent sets of integers like
{ 7, 1, 10, 3, 11, 2, 9, 12, 4}as ordered lists of intervals
[ (1, 5), (7, 8), (9, 13) ]where each pair (i, j) represents the set {i, i+1,..., j-1}.
To verify that the implementation correctly implements a set data type, we need a way to
- Specify the set of values being described,
- Establish some key properties of these sets.
Range-Sets: Semantics of Intervals
We can describe the set of values corresponding
to (i.e. “the semantics of”) an interval i, j
by importing the Data.Set library
88: import qualified Data.Set as S
to write a function rng i j that defines the range-set i..j
94: {-@ reflect rng @-} 95: {-@ rng :: i:Int -> j:Int -> S.Set Int / [j - i] @-} 96: Int -> Int -> (Set Int)rng Inti Intj 97: | {v : Bool | v <=> i < j}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< j = x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union ({v : (Set Int) | v == Set_sng i}S.singleton i) (Int -> Int -> (Set Int)rng (Intix1:Int -> x2:Int -> {v : Int | v == x1 + x2}+1) j) 98: | otherwise = S.empty
The reflect rng tells LH that
we are going to want to work with the Haskell
function rng at the refinement-type level.
Equational Reasoning
To build up a little intuition about the above
definition and how LH reasons about Sets, lets
write some simple unit proofs. For example,
lets check that 2 is indeed in the range-set
rng 1 3, by writing a type signature
116: {-@ test1 :: () -> { S.member 2 (rng 1 3) } @-}
Any implementation of the above type is a proof
that 2 is indeed in rng 1 3. Notice that we can
reuse the operators from Data.Set (here, S.member)
to talk about set operations in the refinement logic.
Lets write this proof in an equational style:
126: () -> {VV : () | Set_mem 2 (RangeSet.rng 1 3)}test1 () 127: = x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member 2 ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng 1 3) 128: -- by unfolding `rng 1 3` 129: === x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member 2 (x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union ((Set Int)S.singleton 1) ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng 2 3)) 130: -- by unfolding `rng 2 3` 131: === x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member 2 (x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union ((Set Int)S.singleton 1) 132: (x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union ((Set Int)S.singleton 2) ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng 3 3))) 133: -- by set-theory 134: === True 135: *** QED
the “proof” uses two library operators:
e1 === e2is an implicit equality that checkse1is indeed equal toe2after unfolding functions at most once, and returns a term that equalse1ande2, ande *** QEDconverts any termeinto a proof.
The first two steps of test1, simply unfold rng
and the final step uses the SMT solver’s
decision procedure for sets to check equalities
over set operations like S.union, S.singleton
and S.member.
Reusing Proofs
Next, lets check that:
160: {-@ test2 :: () -> { S.member 2 (rng 0 3) } @-} 161: () -> {VV : () | Set_mem 2 (RangeSet.rng 0 3)}test2 () 162: = x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member 2 ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng 0 3) 163: -- by unfolding and set-theory 164: === (Bool2 x1:Integer -> x2:Integer -> {v : Bool | v <=> x1 == x2}== 0 {v : x1:Bool -> x2:Bool -> {v : Bool | v <=> x1 || x2} | v == GHC.Classes.||}|| x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member 2 ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng 1 3)) 165: -- by re-using test1 as a lemma 166: ==? True ? {v : () -> {v : () | Set_mem 2 (RangeSet.rng 1 3)} | v == RangeSet.test1}test1 () 167: *** QED
We could do the proof by unfolding in
the equational style. However, test1
already establishes that S.member 2 (rng 1 3)
and we can reuse this fact using:
e1 ==? e2 ? pfan explicit equality which checks thate1equalse2because of the extra facts asserted by theProofnamedpf(in addition to unfolding functions at most once) and returns a term that equals bothe1ande2.
Proof by Logical Evaluation
Equational proofs like test1 and test2
often have long chains of calculations that
can be tedious to spell out. Fortunately, we
taught LH a new trick called
Proof by Logical Evaluation (PLE) that
optionally shifts the burden of performing
those calculations onto the machine. For example,
PLE completely automates the above proofs:
194: {-@ test1_ple :: () -> { S.member 2 (rng 1 3) } @-} 195: () -> {VV : () | Set_mem 2 (RangeSet.rng 1 3)}test1_ple () = () 196: 197: {-@ test2_ple :: () -> { S.member 2 (rng 0 3) } @-} 198: () -> {VV : () | Set_mem 2 (RangeSet.rng 0 3)}test2_ple () = ()
Be Warned! While automation is cool, it can be very helpful to first write out all the steps of an equational proof, at least while building up intuition.
Proof by Induction
At this point, we have enough tools to start proving some
interesting facts about range-sets. For example, if x
is outside the range i..j then it does not belong in
rng i j:
216: {-@ lem_mem :: i:_ -> j:_ -> x:{x < i || j <= x} -> 217: { not (S.member x (rng i j)) } / [j - i] 218: @-}
We will prove the above “by induction”. A confession: I always had trouble understanding what exactly proof by induction really meant. Why was it it ok to “do” induction on one thing but not another?
Induction is Recursion
Fortunately, with LH, induction is just recursion. That is,
We can recursively use the same theorem we are trying to prove, but
We must make sure that the recursive function/proof terminates.
The proof makes this clear:
239: x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {VV : () | not (Set_mem x3 (RangeSet.rng x1 x2))}lem_mem Inti Intj {v : Int | v < i || j <= v}x 240: | {v : Bool | v <=> i >= j}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 >= x2}>= j 241: -- BASE CASE 242: = {v : x1:Bool -> {v : Bool | v <=> not x1} | v == GHC.Classes.not}not (x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member x ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i j)) 243: -- by unfolding 244: === {v : x1:Bool -> {v : Bool | v <=> not x1} | v == GHC.Classes.not}not (x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member x S.empty) 245: -- by set-theory 246: === True *** QED 247: 248: | {v : Bool | v <=> i < j}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< j 249: -- INDUCTIVE CASE 250: = {v : x1:Bool -> {v : Bool | v <=> not x1} | v == GHC.Classes.not}not (x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member x ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i j)) 251: -- by unfolding 252: === {v : x1:Bool -> {v : Bool | v <=> not x1} | v == GHC.Classes.not}not (x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member x (x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union ({v : (Set Int) | v == Set_sng i}S.singleton i) ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng (Intix1:Int -> x2:Int -> {v : Int | v == x1 + x2}+1) j))) 253: -- by set-theory 254: === {v : x1:Bool -> {v : Bool | v <=> not x1} | v == GHC.Classes.not}not (x1:Int -> x2:(Set Int) -> {v : Bool | v <=> Set_mem x1 x2}S.member x ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng (Intix1:Int -> x2:Int -> {v : Int | v == x1 + x2}+1) j)) 255: -- by "induction hypothesis" 256: ==? True ? x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {VV : () | not (Set_mem x3 (RangeSet.rng x1 x2))}lem_mem (Inti x1:Int -> x2:Int -> {v : Int | v == x1 + x2}+ 1) j x *** QED
There are two cases.
Base Case: As
i >= j, we knowrng i jis empty, soxcannot be in it.Inductive Case As
i < jwe can unfoldrng i jand then recursively calllem_mem (i+1) jto obtain the fact thatxcannot be ini+1..jto complete the proof.
LH automatically checks that the proof:
Accounts for all cases, as otherwise the function is not total i.e. like the
headfunction which is only defined on non-empty lists. (Try deleting a case at the demo to see what happens.)Terminates, as otherwise the induction is bogus, or in math-speak, not well-founded. We use the explicit termination metric
/ [j-i]as a hint to tell LH that in each recursive call, the size of the intervalj-ishrinks and is always non-negative. LH checks that is indeed the case, ensuring that we have a legit proof by induction.
Proof by Evaluation
Once you get the hang of the above style, you get tired of spelling out all the details. Logical evaluation lets us eliminate all the boring calculational steps, leaving the essential bits: the recursive (inductive) skeleton
291: {-@ lem_mem_ple :: i:_ -> j:_ -> x:{x < i || j <= x} -> 292: {not (S.member x (rng i j))} / [j-i] 293: @-} 294: x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {VV : () | not (Set_mem x3 (RangeSet.rng x1 x2))}lem_mem_ple Inti Intj {v : Int | v < i || j <= v}x 295: | {v : Bool | v <=> i >= j}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 >= x2}>= j = () 296: | {v : Bool | v <=> i < j}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< j = x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {VV : () | not (Set_mem x3 (RangeSet.rng x1 x2))}lem_mem_ple (Inti x1:Int -> x2:Int -> {v : Int | v == x1 + x2}+ 1) j x
The above is just lem_mem sans the
(PLE-synthesized) intermediate equalities.
Disjointness
We say that two sets are disjoint if their intersection is empty:
309: {-@ inline disjoint @-} 310: disjoint :: S.Set Int -> S.Set Int -> Bool 311: x1:(Set Int) -> x2:(Set Int) -> {VV : Bool | VV <=> Set_cap x1 x2 == Set_empty 0}disjoint (Set Int)a (Set Int)b = x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cap x1 x2}S.intersection a b x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> x1 == x2}== S.empty
Lets prove that two intervals are disjoint if the first ends before the second begins:
318: {-@ lem_disj :: i1:_ -> j1:_ -> i2:{j1 <= i2} -> j2:_ -> 319: {disjoint (rng i1 j1) (rng i2 j2)} / [j2-i2] 320: @-}
This proof goes “by induction” on the size of
the second interval, i.e. j2-i2:
327: x1:Int -> x2:Int -> x3:{i2 : Int | x2 <= i2} -> x4:Int -> {VV : () | Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4) == Set_empty 0}lem_disj Inti1 Intj1 {i2 : Int | j1 <= i2}i2 Intj2 328: | {v : Bool | v <=> i2 >= j2}i2 x1:Int -> x2:Int -> {v : Bool | v <=> x1 >= x2}>= j2 329: -- Base CASE 330: = {v : x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> Set_cap x1 x2 == Set_empty 0} | v == RangeSet.disjoint}disjoint ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i1 j1) ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i2 j2) 331: -- by unfolding 332: === {v : x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> Set_cap x1 x2 == Set_empty 0} | v == RangeSet.disjoint}disjoint ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i1 j1) S.empty 333: -- by set-theory 334: === True 335: *** QED 336: 337: | {v : Bool | v <=> i2 < j2}i2 x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< j2 338: -- Inductive CASE 339: = {v : x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> Set_cap x1 x2 == Set_empty 0} | v == RangeSet.disjoint}disjoint ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i1 j1) ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i2 j2) 340: -- by unfolding 341: === {v : x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> Set_cap x1 x2 == Set_empty 0} | v == RangeSet.disjoint}disjoint ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng i1 j1) (x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union ({v : (Set Int) | v == Set_sng i2}S.singleton i2) ({v : x1:Int -> x2:Int -> {v : (Set Int) | v == RangeSet.rng x1 x2 && v == (if x1 < x2 then Set_cup (Set_sng x1) (RangeSet.rng (x1 + 1) x2) else Set_empty 0)} | v == RangeSet.rng}rng (Inti2x1:Int -> x2:Int -> {v : Int | v == x1 + x2}+1) j2)) 342: -- by induction and lem_mem 343: ==? True ? ({v : x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {v : () | not (Set_mem x3 (RangeSet.rng x1 x2))} | v == RangeSet.lem_mem}lem_mem i1 j1 i2 {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& x1:Int -> x2:Int -> x3:{i2 : Int | x2 <= i2} -> x4:Int -> {VV : () | Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4) == Set_empty 0}lem_disj i1 j1 (Inti2x1:Int -> x2:Int -> {v : Int | v == x1 + x2}+1) j2) 344: *** QED
Here, the operator pf1 &&& pf2 conjoins the
two facts asserted by pf1 and pf2.
Again, we can get PLE to do the boring calculations:
353: {-@ lem_disj_ple :: i1:_ -> j1:_ -> i2:{j1 <= i2} -> j2:_ -> 354: {disjoint (rng i1 j1) (rng i2 j2)} / [j2-i2] 355: @-} 356: x1:Int -> x2:Int -> x3:{i2 : Int | x2 <= i2} -> x4:Int -> {VV : () | Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4) == Set_empty 0}lem_disj_ple Inti1 Intj1 {i2 : Int | j1 <= i2}i2 Intj2 357: | {v : Bool | v <=> i2 >= j2}i2 x1:Int -> x2:Int -> {v : Bool | v <=> x1 >= x2}>= j2 = () 358: | {v : Bool | v <=> i2 < j2}i2 x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< j2 = {v : x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {v : () | not (Set_mem x3 (RangeSet.rng x1 x2))} | v == RangeSet.lem_mem}lem_mem i1 j1 i2 {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& x1:Int -> x2:Int -> x3:{i2 : Int | x2 <= i2} -> x4:Int -> {VV : () | Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4) == Set_empty 0}lem_disj_ple i1 j1 (Inti2x1:Int -> x2:Int -> {v : Int | v == x1 + x2}+1) j2
Splitting Intervals
Finally, we can establish the splitting property
of an interval i..j, that is, given some x that lies
between i and j we can split i..j into i..x
and x..j. We define a predicate that a set s can
be split into a and b as:
372: {-@ inline split @-} 373: split :: S.Set Int -> S.Set Int -> S.Set Int -> Bool 374: x1:(Set Int) -> x2:(Set Int) -> x3:(Set Int) -> {VV : Bool | VV <=> x1 == Set_cup x2 x3 && Set_cap x2 x3 == Set_empty 0}split (Set Int)s (Set Int)a (Set Int)b = Bools x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> x1 == x2}== x1:(Set Int) -> x2:(Set Int) -> {v : (Set Int) | v == Set_cup x1 x2}S.union a b {v : x1:Bool -> x2:Bool -> {v : Bool | v <=> x1 && x2} | v == GHC.Classes.&&}&& {v : x1:(Set Int) -> x2:(Set Int) -> {v : Bool | v <=> Set_cap x1 x2 == Set_empty 0} | v == RangeSet.disjoint}disjoint a b
We can now state and prove the splitting property as:
380: {-@ lem_split :: i:_ -> x:{i <= x} -> j:{x <= j} -> 381: {split (rng i j) (rng i x) (rng x j)} / [x-i] 382: @-} 383: x1:Int -> x2:{v : Int | x1 <= v} -> x3:{j : Int | x2 <= j} -> {VV : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0}lem_split Inti {v : Int | i <= v}x {j : Int | x <= j}t 384: | {v : Bool | v <=> i == x}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 == x2}== x = () 385: | {v : Bool | v <=> i < x}i x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< x = x1:Int -> x2:{v : Int | x1 <= v} -> x3:{j : Int | x2 <= j} -> {VV : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0}lem_split (Inti x1:Int -> x2:Int -> {v : Int | v == x1 + x2}+ 1) x t {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:Int -> x3:{v : Int | v < x1 || x2 <= v} -> {v : () | not (Set_mem x3 (RangeSet.rng x1 x2))} | v == RangeSet.lem_mem}lem_mem x t i
(We’re using PLE here quite aggressively, can you work out the equational proof?)
Set Operations
The splitting abstraction is a wonderful hammer that lets us break higher-level proofs into the bite sized pieces suitable for the SMT solver’s decision procedures.
Subset
An interval i1..j1 is enclosed by i2..j2
if i2 <= i1 < j1 <= j2. Lets verify that the
range-set of an interval is contained in
that of an enclosing one.
406: {-@ lem_sub :: i1:_ -> j1:{i1 < j1} -> 407: i2:_ -> j2:{i2 < j2 && i2 <= i1 && j1 <= j2 } -> 408: { S.isSubsetOf (rng i1 j1) (rng i2 j2) } 409: @-}
Here’s a “proof-by-picture”. We can split the
larger interval i2..j2 into smaller pieces,
i2..i1, i1..j1 and j1..j2 one of which
is the i1..j1, thereby completing the proof:

The intuition represented by the picture can distilled
into the following proof, that invokes lem_split to
carve i2..j2 into the relevant sub-intervals:
432: x1:Int -> x2:{j1 : Int | x1 < j1} -> x3:Int -> x4:{j2 : Int | x3 < j2 && x3 <= x1 && x2 <= j2} -> {VV : () | Set_sub (RangeSet.rng x1 x2) (RangeSet.rng x3 x4)}lem_sub Inti1 {j1 : Int | i1 < j1}j1 Inti2 {j2 : Int | i2 < j2 && i2 <= i1 && j1 <= j2}j2 = {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i2 i1 j2 {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i1 j1 j2
Union
An interval i1..j1 overlaps i2..j2
if i1 <= j2 <= i2, that is, if the latter
ends somewhere inside the former.
The same splitting hammer lets us compute
the union of two overlapping intervals
simply by picking the interval defined
by the endpoints.
446: {-@ lem_union :: 447: i1:_ -> j1:{i1 < j1} -> 448: i2:_ -> j2:{i2 < j2 && i1 <= j2 && j2 <= j1 } -> 449: { rng (min i1 i2) j1 = S.union (rng i1 j1) (rng i2 j2) } 450: @-}
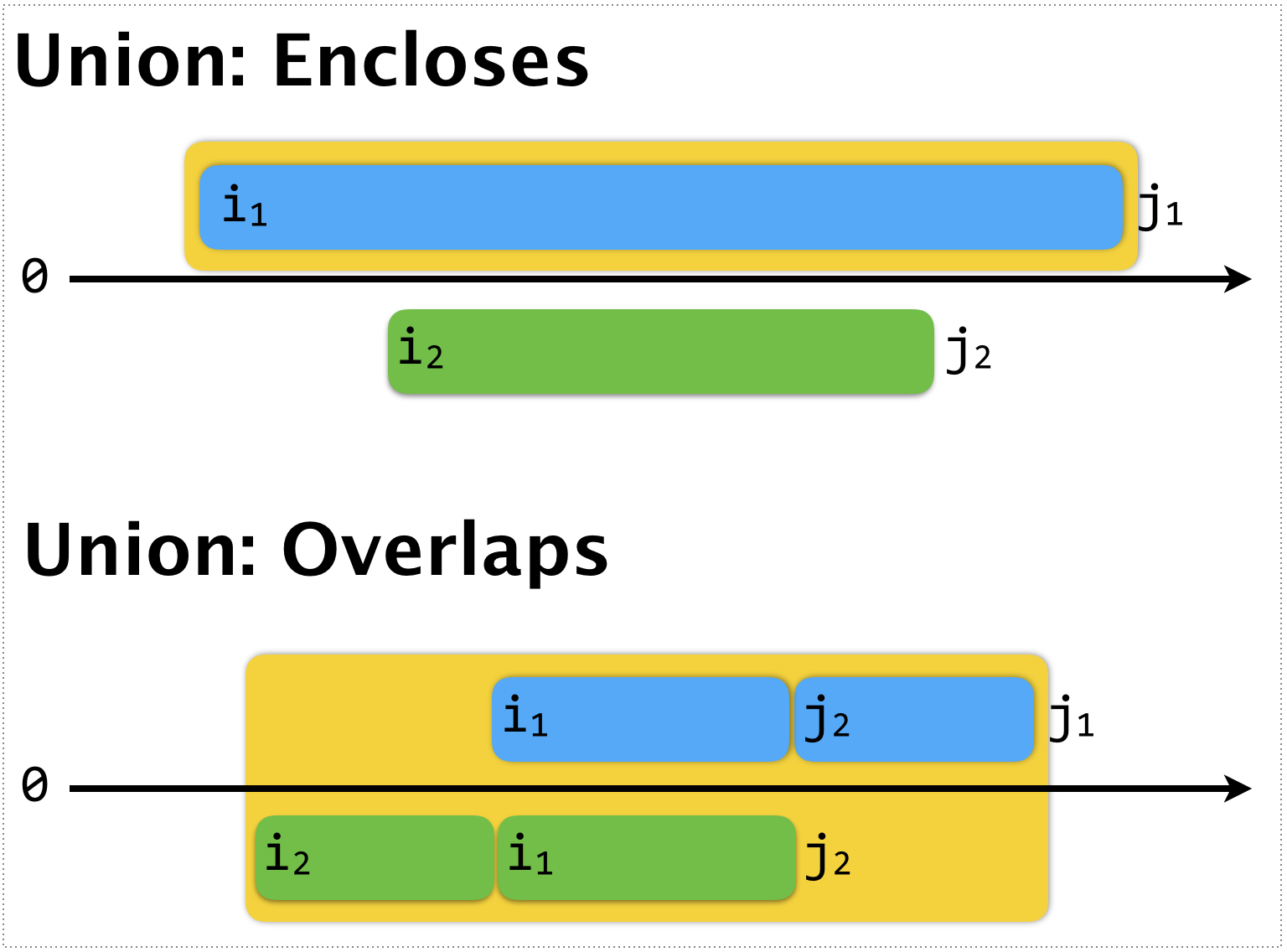
The pictorial proof illustrates the two cases:
i1..j1enclosesi2..j2; here the union is justi1..j1,i1..j1only overlapsi1..j1; here the union isi2..j1which can be split intoi2..i1,i1..j2andj2..j1which are exactly the union of the intervalsi1..j1andi2..j2.
Again, we render the picture into a formal proof as:
474: x1:Int -> x2:{j1 : Int | x1 < j1} -> x3:Int -> x4:{j2 : Int | x3 < j2 && x1 <= j2 && j2 <= x2} -> {VV : () | RangeSet.rng (RangeSet.min x1 x3) x2 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x3 x4)}lem_union Inti1 {j1 : Int | i1 < j1}j1 Inti2 {j2 : Int | i2 < j2 && i1 <= j2 && j2 <= j1}j2 475: -- i1..j1 encloses i2..j2 476: | {v : Bool | v <=> i1 < i2}i1 x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< i2 = {v : x1:Int -> x2:{v : Int | x1 < v} -> x3:Int -> x4:{v : Int | x3 < v && x3 <= x1 && x2 <= v} -> {v : () | Set_sub (RangeSet.rng x1 x2) (RangeSet.rng x3 x4)} | v == RangeSet.lem_sub}lem_sub i2 j2 i1 j1 477: -- i1..j1 overlaps i2..j2 478: | otherwise = {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i2 i1 j1 479: {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i1 j2 j1 480: {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i2 i1 j2
Intersection
Finally, we check that the intersection of two overlapping intervals is given by their inner-points.
489: {-@ lem_intersect :: 490: i1:_ -> j1:{i1 < j1} -> 491: i2:_ -> j2:{i2 < j2 && i1 <= j2 && j2 <= j1 } -> 492: {rng (max i1 i2) j2 = S.intersection (rng i1 j1) (rng i2 j2)} 493: @-}
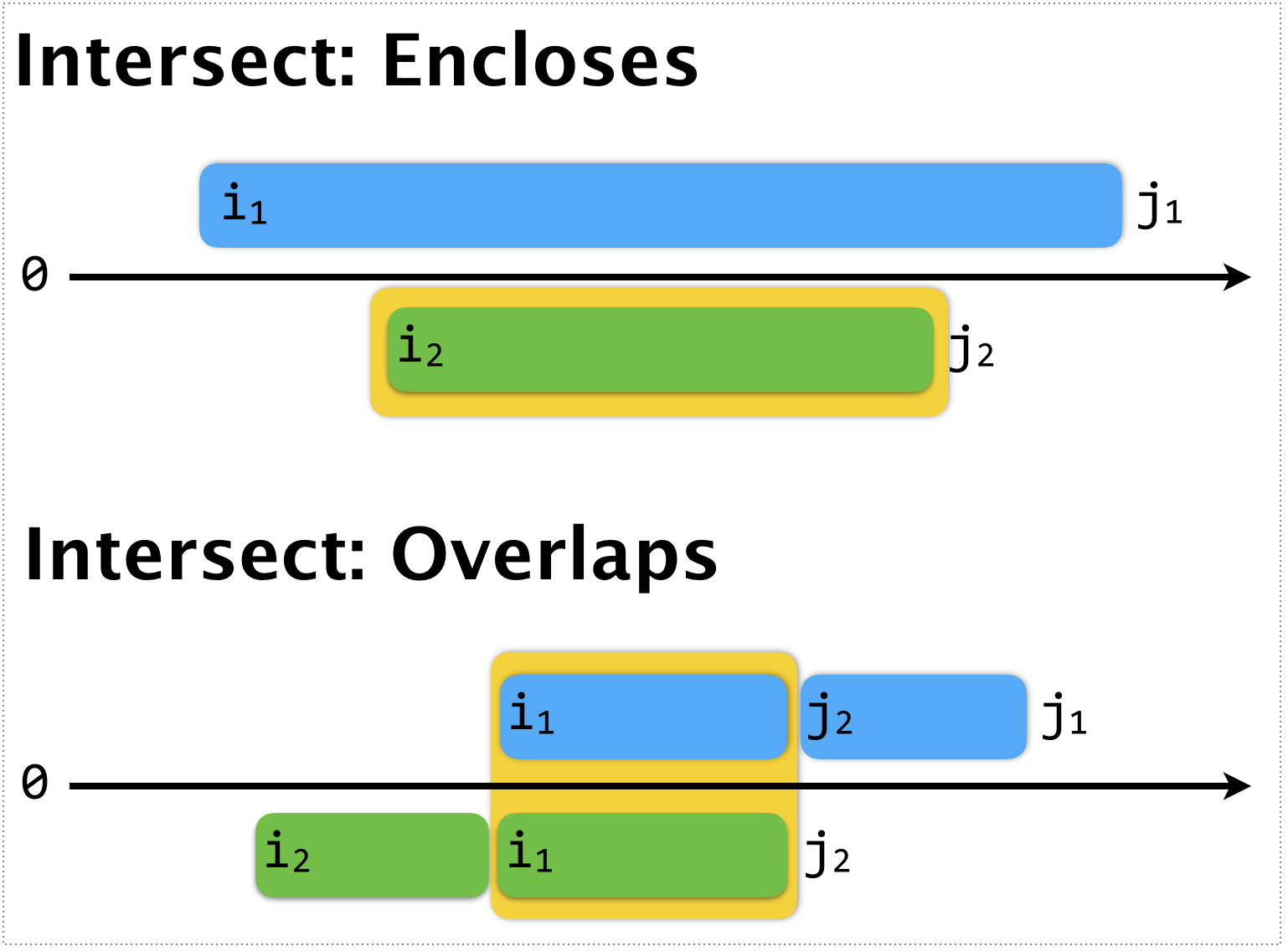
We have the same two cases as for lem_union
i1..j1enclosesi2..j2; here the intersection is justi2..j2,i1..j1only overlapsi1..j1; here the intersection is the middle segmenti1..j2, which we obtain by- splitting
i1..j1atj2, - splitting
i2..j2ati1, - discarding the end segments which do not belong in the intersection.
- splitting
517: x1:Int -> x2:{j1 : Int | x1 < j1} -> x3:Int -> x4:{j2 : Int | x3 < j2 && x1 <= j2 && j2 <= x2} -> {VV : () | RangeSet.rng (RangeSet.max x1 x3) x4 == Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4)}lem_intersect Inti1 {j1 : Int | i1 < j1}j1 Inti2 {j2 : Int | i2 < j2 && i1 <= j2 && j2 <= j1}j2 518: -- i1..j1 encloses i2..j2 519: | {v : Bool | v <=> i1 < i2}i1 x1:Int -> x2:Int -> {v : Bool | v <=> x1 < x2}< i2 = {v : x1:Int -> x2:{v : Int | x1 < v} -> x3:Int -> x4:{v : Int | x3 < v && x3 <= x1 && x2 <= v} -> {v : () | Set_sub (RangeSet.rng x1 x2) (RangeSet.rng x3 x4)} | v == RangeSet.lem_sub}lem_sub i2 j2 i1 j1 520: -- i1..j1 overlaps i2..j2 521: | otherwise = {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i1 j2 j1 522: {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:{v : Int | x1 <= v} -> x3:{v : Int | x2 <= v} -> {v : () | RangeSet.rng x1 x3 == Set_cup (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) && Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x2 x3) == Set_empty 0} | v == RangeSet.lem_split}lem_split i2 i1 j2 523: {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:Int -> x3:{v : Int | x2 <= v} -> x4:Int -> {v : () | Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4) == Set_empty 0} | v == RangeSet.lem_disj}lem_disj i2 i1 i1 j1 -- discard i2..i1 524: {v : () -> () -> () | v == Language.Haskell.Liquid.NewProofCombinators.&&&}&&& {v : x1:Int -> x2:Int -> x3:{v : Int | x2 <= v} -> x4:Int -> {v : () | Set_cap (RangeSet.rng x1 x2) (RangeSet.rng x3 x4) == Set_empty 0} | v == RangeSet.lem_disj}lem_disj i2 j2 j2 j1 -- discard j2..j1
Conclusions
Whew. That turned out a lot longer than I’d expected!
On the bright side, we saw how to:
- Specify the semantics of range-sets,
- Write equational proofs using plain Haskell code,
- Avoid boring proof steps using PLE,
- Verify key properties of operations on range-sets.
Next time we’ll finish the series by showing how to use the above lemmas to specify and verify the correctness of Breitner’s implementation.
547: -------------------------------------------------------------------------------- 548: -- | Some helper definitions 549: -------------------------------------------------------------------------------- 550: {-@ reflect min @-} 551: min :: (Ord a) => a -> a -> a 552: (Ord a) => x2:a -> x3:a -> {VV : a | VV == RangeSet.min x2 x3 && VV == (if x2 < x3 then x2 else x3)}min ax ay = {v : Bool | v <=> x < y}if {v : Bool | v <=> x < y}x x1:a -> x2:a -> {v : Bool | v <=> x1 < x2}< y then x else y 553: 554: {-@ reflect max @-} 555: max :: (Ord a) => a -> a -> a 556: (Ord a) => x2:a -> x3:a -> {VV : a | VV == RangeSet.max x2 x3 && VV == (if x2 < x3 then x3 else x2)}max ax ay = {v : Bool | v <=> x < y}if {v : Bool | v <=> x < y}x x1:a -> x2:a -> {v : Bool | v <=> x1 < x2}< y then y else x 557: 558: rng :: Int -> Int -> S.Set Int 559: test1 :: () -> () 560: test2 :: () -> () 561: test1_ple :: () -> () 562: test2_ple :: () -> () 563: lem_mem :: Int -> Int -> Int -> () 564: lem_mem_ple :: Int -> Int -> Int -> () 565: lem_sub :: Int -> Int -> Int -> Int -> () 566: lem_disj :: Int -> Int -> Int -> Int -> () 567: lem_disj_ple :: Int -> Int -> Int -> Int -> () 568: lem_split :: Int -> Int -> Int -> () 569: 570: lem_intersect :: Int -> Int -> Int -> Int -> () 571: lem_union :: Int -> Int -> Int -> Int -> () 572: -- https://ucsd-progsys.github.io/liquidhaskell-blog/tags/induction.html 573:
