CSE 130

Generics (Subtyping + Parametric Polymorphism)

Ranjit Jhala, UC San Diego

Announcements

Course Evaluations

CAPE

Fill this out!

Topics

OCaml: ~20 lectures and 4 homeworks

Scala: ~10 lectures and 2 homeworks

The exam will reflect this difference in time spent.

Be generally comfortable with the Scala material and assignments...

Final Exam

Practice Questions

Will be posted on webpage

Review Session

Stay tuned on PIAZZA

Come prepared with questions!

A Tale of Two Polymorphisms

Subtype Polymorphism ("Is-A" style; classic OO)

Parametric Polymorphism ("Type Variables"; ML style)

Scala combines them in interesting ways.

Today's Plan

Parametric Polymorphism ("Type Variables"; ML style)

Functions

Classes/Traits

Combining Subtyping + Parametric Polymorphism

Proxies and Implicits

Retrofitting behavior to existing types.

Functions with Type Variables

Parametrically Polymorphic Functions

Unlike OCaml, you have to write down the type variables:

/* val id : 'a -> 'a
/* OCaml: let id x = x */

scala> def id[A](x:A) = x
id: [A](x: A)A

/* val swap : ('a, 'b) -> ('b, 'a) */
/* OCaml: let swap (x, y) = (y, x) */
scala> def swap[A,B](p: (A,B)) = (p._2, p._1)
swap: [A, B](p: (A, B))(B, A)

Recall: 'a -> 'a in OCaml really meant "forall 'a. 'a -> 'a"

In Scala, you have to write the "forall" part with [...]

Parametrically Polymorphic Functions

At function call, can explicitly instantiate the type parameters:

scala> swap[Int, Boolean](1, true)
res10: (Boolean, Int) = (true,1)

But often, local type inference can implicitly instantiate them:

scala> swap(1, true)
res11: (Boolean, Int) = (true,1)

Parametrically Polymorphic Lists

Recall the type ascription expression from last time.

scala> List()
res17: List[Nothing] = List()

scala> List(): List[Int]
res18: List[Int] = List()

scala> List(): List[Boolean]
res19: List[Boolean] = List()

scala> List(): List[List[Int]]
res20: List[List[Int]] = List()

Parametrically Polymorphic Lists

Recall the type ascription expression from last time.

scala> Nil
res23: scala.collection.immutable.Nil.type = List()

scala> Nil: List[Int]
res24: List[Int] = List()

scala> Nil: List[Boolean]
res25: List[Boolean] = List()

scala> Nil: List[List[Int]]
res26: List[List[Int]] = List()

Parametrically Polymorphic Lists

Wait, there are two ways to describe the empty list?

scala> Nil: List[Int]
res24: List[Int] = List()

scala> List(): List[Int]
res18: List[Int] = List()

scala> Nil == List()
res32: Boolean = true

Remember OCaml Datatypes?

Datatypes in OCaml were awesome.

# type t = A | B ;;

Compiler figured out inexhaustive and redundant patterns:

# let foo x = match x with A -> () ;;     
Warning: this pattern-matching is not exhaustive.
foo : t -> unit

# let bar x = match x with A -> () | B -> () | B -> () ;;
Warning: this match case is unused.
bar : t -> unit

Datatypes vs. Classes

OCaml Datatypes

# type t = A | B ;;

Easy to define new operation (foo, bar, baz) for every t-typed value.

Scala Classes

class t
class A() extends t
class B() extends t

Easy to define new kind (sub-class A, B, C) of t-typed value.

Can we have the best of both?

Case Classes

A mix of classes and datatypes...

class t
case class A() extends t
case class B() extends t

... that enables pattern matching!

def foo(x: t) = x match {
  case A() => println("A")
  case B() => println("B")
}

CLICKER: Case Classes

class t
case class A() extends t

def bar(x: t) = x match {
  case A() => println("A")
  case A() => println("A")
}

What is the result of evaluating bar?

A: Type Error

B: t -> Unit

C: t -> Unit with a warning

Case Classes

class t
case class A() extends t

def bar(x: t) = x match {
  case A() => println("A")
  case A() => println("A")
}

Scala has no problem detecting redundant cases.

C: t -> Unit with a warning

CLICKER: Case Classes

class t
case class A() extends t
case class B() extends t

def baz(x: t) = x match {
  case A() => println("A")
}

What is the result of evaluating bar?

A: Type Error

B: t -> Unit

C: t -> Unit with a warning

Case Classes

class t
case class A() extends t
case class B() extends t

def baz(x: t) = x match {
  case A() => println("A")
}

B: t -> Unit (with no warning)

Why can't Scala figure out inexhaustive pattern match?

Because subclasses can be defined anywhere later!

Sealed Classes

If a (regular or case) class is marked as sealed...

sealed class t
case class A() extends t
case class B() extends t

Then all subclasses must appear in the same file.

They may not appear anywhere else.

So the following leads to compile-time warning:

def baz(x: t) = x match {
  case A() => println("A")
}

Parametric Polymorphism: List Length

(* ML *)
let rec length xs = match xs with
  | []   -> 0
  | _::t -> 1 + length t

/* Scala */
def length[A](xs: List[A]): Int =
  xs match {
    case Nil      => 0
    case (_ :: t) => 1 + length(t)
  }

Parametric Polymorphism: List Map

(* ML *)
let rec map f xs = match xs with
  | []   -> []
  | x::t -> (f x) :: map (f, t)

/* Scala */
def map[A, B](f: A => B)(xs: List[A]): List[B] =
  xs match {
    case Nil      => List()
    case (_ :: t) => (f(x))::(map(f)(t))
  }

Are These Functions Equivalent?

// Subtype Polymorphism
def headAny(xs: List[Any]): Any =
  xs match {
    case h :: _ => h
    case _      => sys.error("head of empty list")
  }

// Parametric Polymorphism
def headPoly[A](xs: List[A]): A =
  xs match {
    case h :: _ => h
    case _      => sys.error("head of empty list")
  }

They seem to behave the same, but types are different...

Are These Functions Equivalent?

// Subtype Polymorphism
def headAny(xs: List[Any]): Any = ...

// Parametric Polymorphism
def headPoly[A](xs: List[A]): A = ...

They can both be called with any type of list...

But the return type of headAny is very imprecise.

Whereas the return type of headPoly is very precise.

Are These Functions Equivalent?

// Subtype Polymorphism
def headAny(xs: List[Any]): Any = ...

// Parametric Polymorphism
def headPoly[A](xs: List[A]): A = ...

scala> val ns = List(1,2,3)
ns: List[Int] = List(1, 2, 3)

scala> val (i, j) = (headAny(ns), headPoly(ns))
i: Any = 1
j: Int = 1

Classes/Traits with Type Variables

Parametrically Polymorphic Classes

We've already hinted at this with List[A].

Now let's see how to define a class with type variables.

Our running example will be polymorphic sets (a.k.a "bags").

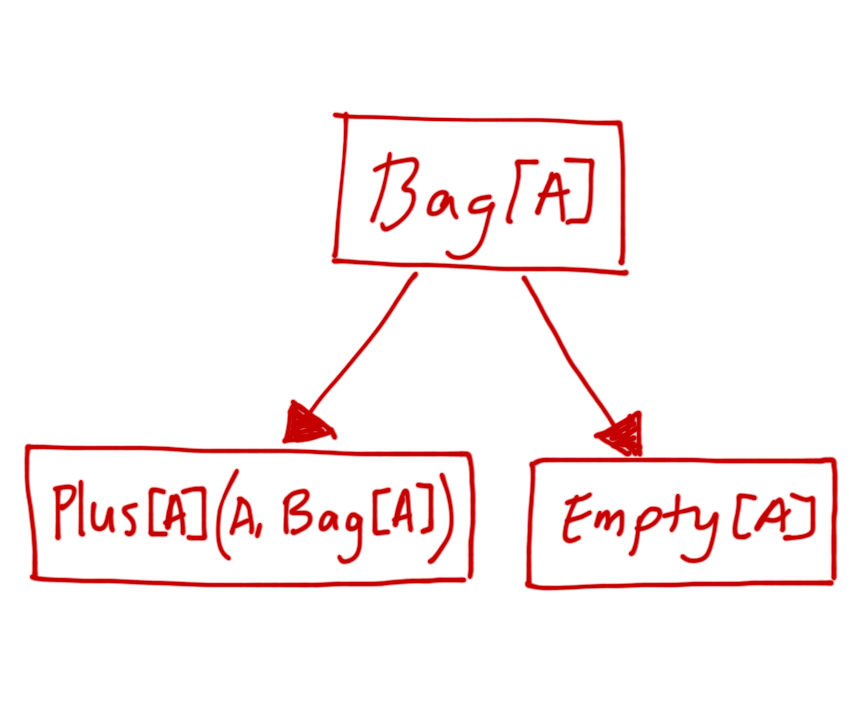
UnorderedBag.scala

Parametrically Polymorphic Classes

sealed abstract class Bag[A]
case class Empty[A]() extends Bag[A]
case class Plus[A](elt: A, rest: Bag[A]) extends Bag[A]

Very similar to what you might write in OCaml:

type 'a bag = Empty | Plus of ('a * 'a bag)

Parametrically Polymorphic Classes

sealed abstract class Bag[A]
case class Empty[A]()                    extends Bag[A]
case class Plus[A](elt: A, rest: Bag[A]) extends Bag[A]

Case Classes are Just Vanilla Classes...

But no need for pesky new to create instances

But also support pattern matching

Parametrically Polymorphic Classes

sealed abstract class Bag[A]
case class Empty[A]()                    extends Bag[A]
case class Plus[A](elt: A, rest: Bag[A]) extends Bag[A]

Parametrically Polymorphic Classes

We can fill in various methods...

sealed abstract class Bag[A] {
  ...
  def size : Int =
    this match {
      case Empty()       => 0
      case Plus(_, rest) => 1 + rest.size
    }
  ...
}

The this expression denotes the receiver bag.

Parametrically Polymorphic Classes

We can fill in various methods...

sealed abstract class Bag[A] {
  // ...
  def contains(x: A) : Boolean = {
    this match {
      case Empty()                => false
      case Plus(e, _) if (x == e) => true  
      case Plus(_, rest)          => rest.contains(x)
    }
  }
  // ...
}

Type parameter A is in scope in entire class definition.

Parametrically Polymorphic Classes

We can fill in various methods...

sealed abstract class Bag[A] {
  // ...
  def add(x: A) : Bag[A] = {
    if (this.contains(x)) this else { Plus(x, this) }
  }
  // ...
}

A brand new, immutable Bag returned as output.

Parametrically Polymorphic Classes

We can fill in various methods...

sealed abstract class Bag[A] {
  // ...
  def gimme: Option[A] =
    this match {
      case Plus(x, rest) => Some(x)
      case _             => None
    }
  // ...
}

Element is not removed from this bag.

Today's Plan

Parametric Polymorphism ("Type Variables"; ML style)

Functions
Classes/Traits

Combining Subtyping + Parametric Polymorphism

Proxies and Implicits

Combining Subtyping
+ Parametric Polymorphism

CLICKER: What is the value of `res`?

def findMin[A](cur: A, xs: List[A]): A = xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
}

val res = findMin(1000, List(20, 4, 1, 6))

A. Type Error in findMin(1000, ...)

B. Type Error in definition of findMin

C. Type Error in List(20,4,1,6)

D. 1

E. 20

What is the value of `res`?

def findMin[A <: Ord[A]](cur: A, xs: List[A]): A = xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
}

val res = findMin(1000, List(20, 4, 1, 6))

B. Type Error in definition of findMin

error: value < is not a member of type parameter A
           case h::t if (h < cur) => findMin(h, t)
                           ^

Want to describe WHICH types
support comparison...

Traits!

trait Ord[A] {
  def cmp(that: A): Int // Must Be Implemented ...

  // ... Automatically derived from cmp !
  def ===(that: A): Boolean = (this cmp that) == 0
  def <(that: A): Boolean   = (this cmp that) < 0
  def >(that: A): Boolean   = (this cmp that) > 0
  def <=(that: A): Boolean  = (this cmp that) <= 0
  def >=(that: A): Boolean  = (this cmp that) <= 0
}

Ord.scala

From one required method, we get a bunch of methods for free!

(Similar to type classes in Haskell.)

An Ordered List...

def findMin[???](cur: ???, xs: List[???]): ??? =
  xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
  }

We want to say any type A... (parametric polymorphism)

That is a subtype of Ord. (subtyping)

Combine both kinds of polymorphism with bounded quantification.

[A <: Ord[A]]

An Ordered List... with Bounded Quantification

def findMin[A <: Ord[A]](cur: A, xs: List[A]): A =
  xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
  }

We'll come back to this example in a bit...

But first, let's make an ordered version of Bag.

`Bag` is a pretty lame data structure

contains, add, etc.

Must walk over entire bag to determine if elements are present.

Let us arrange the elements in increasing order ...

... can tell if an element is absent when we find a bigger one.

Note: this is starting to sound like Bst in Homework 6...

An Ordered `Bag`

sealed abstract class Bag[A <: Ord[A]] {
  // ...
}

For every A that is a subtype of Ord[A] (i.e. that implements Ord[A])

We define the methods of Bag[A]

An Ordered Bag

A faster version of contains that does not walk the entire bag.

sealed abstract class Bag[A <: Ord[A]] {
  // ...
  def contains(x: A) : Boolean =
    this match {
      case Empty()                => false
      case Plus(e, _) if (x == e) => true  
      case Plus(e, _) if (x  > e) => false
      case Plus(_, rest)          => rest.contains(x)
  }
  // ...
}

An Ordered Bag

... Assuming that elements are ordered in the first place!

So, we must change the add method to enforce this invariant.

sealed abstract class Bag[A <: Ord[A]] {
  // ...
  def add(x: A) : Bag[A] =
    this match {
      case Plus(e, es) if (x > e)  => Plus(e, es.add(x))
      case Plus(e, _)  if (x == e) => this
      case _                       => Plus(x, this)
    }
  // ...
}

An Ordered Bag

The remove method can also be made a bit more efficient.

No need to go to the end:

sealed abstract class Bag[A <: Ord[A]] {
  // ...
  def remove(x: A) : Bag[A] =
   this match {
    case Plus(e, es) if (x <  e) => this
    case Empty()                 => this
    case Plus(e, es) if (x == e) => es
    case Plus(e, es)             => Plus(e, es.remove(x))
  }
  // ...
}

RECAP: Bounded Quantification

[A <: T] describes

All types A... (parametric polymorphism)

That are subtypes of T. (subtyping)

CLICKER: What is the value of `res`?

def findMin(cur: A, xs: List[A]): A =
  xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
  }

val res = findMin(1000, List(20, 4, 1, 6))

A. Type Error in findMin(1000, ...)

B. Type Error in definition of findMin

C. 1

What is the value of `res`?

def findMin[A <: Ord[A]](cur: A, xs: List[A]): A =
  xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
  }

val res = findMin(1000, List(20, 4, 1, 6))

When call instantiates A with type argument Int,

Scala checks if Int is a subtype of Ord[Int].

But we just defined Ord...

So of course Int is not a subtype of Ord[Int]!

What is the value of `res`?

A. Type Error in findMin(1000, ...)

scala> val res = findMin(1000, List(1,2,3))
error: inferred type arguments [Int] do not conform to
       method findMin's type parameter bounds
       [A <: Ord[A]]

Explicit type argument makes no difference.

scala> val res = findMin[Int](1000, List(1,2,3))
error: type arguments [Int] do not conform to
       method findMin's type parameter bounds
       [A <: Ord[A]]

How to Add Functionality to Existing Types?

Today's Plan

Parametric Polymorphism ("Type Variables"; ML style)

Functions
Classes/Traits

Combining Subtyping + Parametric Polymorphism

Proxies and Implicits

Retrofitting Functionality with Proxies

Retrofitting Functionality with Proxies




trait Wierd {
  def godZilla : Int
}

def foo(x : Wierd) = println("Sooo wierd")

def findMin[A](cur: A, xs: List[A])(implicit sideKick: A => Ord[A]): A =
  xs match {
    case Nil               => cur
    case h::t if (h < cur) => findMin(h, t)
    case _::t              => findMin(cur, t)
  }

implicit def intSideKick(x:Int) = new Ord[Int] {
  def cmp(that : Int) = x - that
  }

implicit def strSideKick(x:String) = new Ord[String] {
  def cmp(that : String) = x compare that
  }


Will it work?

A. Yes
B. No

Now, the Int need not itself implement Ord[Int]

i.e. Int need not support comparisons with Int

But some proxy must be able to do comparisons on its behalf...

Let's create such a proxy function!

Retrofitting Functionality with Proxies

def findMin[A](cur: A, xs: List[A])(proxy: A => Ord[A]) =
  xs match {
    case Nil                      => cur
    case h::t if (proxy(h) < cur) => findMin(h, t)
    case _::t                     => findMin(cur, t)
  }

def intProxy(x: Int) = new Ord[Int] {
  def cmp(that: Int) : Int = x - that
}

maps x: Int to an Ord[Int] object supporting comparisons with x

Retrofitting Functionality with Proxies

def findMin[A](cur: A, xs: List[A])(proxy: A => Ord[A]) =
  xs match {
    case Nil                      => cur
    case h::t if (proxy(h) < cur) => findMin(h, t)(proxy)
    case _::t                     => findMin(cur, t)(proxy)
  }

def intProxy(x: Int) = new Ord[Int] {
  def cmp(that: Int) : Int = x - that
}

scala> import ProxyDemo._
scala> findMin(1000, List(20, 4, 1, 6))(intProxy)
res1: Int = 1

Retrofitting Functionality with Proxies

Of course, we can create proxies for other types, too:

def stringProxy(x: String) = new Ord[String] {
  def cmp(that: String) : Int = x compare that
}

scala> import ProxyDemo._
scala> findMin("zz", List("apple", "chorizo", "adobado"))
              (stringProxy)
res1: String = "adobado"

Retrofitting Functionality with Proxies

Proxies are Awesome

Add functionality to existing types by letting us view

Int as implementation of Ord[Int]

String as implementation of Ord[String]

... But Proxies are Also Lame

Proxies require us to

Pass around the relevant proxy functions ...

Clutter code with ugly conversions ...

Let's Keep the Awesome and
Eliminate the Lame

Implicit Parameters and Values

// Mark certain function params as implicit
def sayHello(implicit n: String) = println("Hello " + n)

// Mark certain values as implicit
implicit val defaultName = "Ranjit"

Can call the functions in the usual way:

scala> sayHello("Roberto")
Hello Roberto

Implicit Parameters and Values

// Mark certain function params as implicit
def sayHello(implicit n: String) = println("Hello " + n)

// Mark certain values as implicit
implicit val defaultName = "Ranjit"

Can call the functions in the usual way:

scala> sayHello("Roberto")
Hello Roberto

Otherwise, Scala fills in the blanks:

scala> sayHello
Hello Ranjit

Implicits: The Magic of Types

Scala uses types to fill in the blanks.

When missing a value of type T

Scala automatically substitutes implicit T value ...

... if such a value is in scope.

Implicits: Automatically "Fix" Type Errors

Suppose I wrote a function expecting String inputs

scala> def yu(msg: String) = println("Y U  NO " + msg)
yu: (msg: String)Unit

Naturally, this is fine ...

scala> yu("GIVE EASY FINAL")
Y U  NO GIVE EASY FINAL

... but this throws an error

scala> yu(10)
<console>:9: error: type mismatch;
 found   : Int(10)
 required: String
       yu(10)
          ^

Implicits: Automatically "Fix" Type Errors

Suppose I wrote a function expecting String inputs

scala> def yu(msg: String) = println("Y U  NO " + msg)
yu: (msg: String)Unit

But if we add an implicit conversion

scala> implicit def i2s(i: Int) = i.toString
i2s: (i: Int)java.lang.String

Then lo and behold!

scala> yu(10)       
Y U  NO 10

yu(10) fixed to yu(int2String(10))

Using the type mismatch and type of i2s

Retrofitting Functionality

Proxies require we pass around functions & clutter code...

Implicits automatically insert proxies where needed!

Retrofitting Functionality with Implicit Proxies

Step 1: Make proxy parameters implicit

def findMin[A](cur: A, xs: List[A])
              (implicit proxy: A => Ord[A]): A =
 xs match {
   case Nil                      => cur
   case h::t if (proxy(h) < cur) => findMin(h, t)(proxy)
   case _::t                     => findMin(cur, t)(proxy)
 }

Retrofitting Functionality with Implicit Proxies

Step 2: Remove explicit uses of proxy

(Scala automatically inserts them!)

def findMin[A](cur: A, xs: List[A])
              (implicit proxy: A => Ord[A]): A =
 xs match {
   case Nil                        => cur
   case h::t if (/*proxy*/h < cur) => findMin(h, t)
   case _::t                       => findMin(cur, t)
 }

Retrofitting Functionality with Implicit Proxies

Step 3: Make proxy functions implicit

implicit def intProxy(x: Int) = new Ord[Int] {
  def cmp(that: Int) : Int = x - that
}

implicit def stringProxy(x: String) = new Ord[String] {
  def cmp(that: String) : Int = x compare that
}

Retrofitting Functionality with Implicit Proxies

Make proxy parameters implicit.
Remove explicit uses of proxy. (Scala automatically inserts them!)
Make proxy functions implicit.

scala> val res = // look ma, no proxies!
         findMin(1000, List(10, 2, 30, 14))
res: Int = 2

Retrofitting Functionality with Implicit Proxies

This pattern is so common that it warrants special syntax.

Instead of:

def findMin[A](cur: A, xs: List[A])
              (implicit proxy: A => Ord[A]): A

We can just write the equivalent:

def findMin[A <% Ord[A]](cur: A, xs: List[A]): A

Called a View Bound. A <% Ord[A]

For any A with an implicit proxy mapping A to Ord[A]

(Deprecated) as an "anti-pattern"

Retrofitting Functionality with Implicit Proxies

We can now make a real ordered bag

sealed abstract class Bag[A <% Ord[A]] {

  def contains(x: A) : Boolean = {
    this match {
      case Empty()                => false
      case Plus(e, _) if (x == e) => true  
      case Plus(e, _) if (x  > e) => false
      case Plus(_, rest)          => rest.contains(x)
    }
  }

  // etc.

(Again, this is an "anti-pattern")

Today's Plan: A Tale of Two Polymorphisms

Parametric Polymorphism ("type variables", ML style)
- def add[A](x: A): Bag[A]
Subtyping + Parametric Polymorphism
- def add[A <: Ord[A]](x: A): Bag[A]
Implicitly retrofitting behavior to existing types
- def add[A <% Ord[A]](x: A): Bag[A]

Types enable reuse without compromising safety

See the code

Typeclass Pattern

Why not Implicit Proxies?

Implicit proxies are great, but they become confusing in large code-bases

Why not Implicit Proxies?

Implicit proxies are great, but they become confusing in large code-bases

trait Cool130App {
  implicit def intProxy(x: Int) = new Ord[Int] {
    def cmp(that: Int) : Int = x - that
  }
}

object Test extends Cool130App {
  val tb = Bag(2,3,4)
}

Where did the implicit come from in Test?

What if we didn't have the source for Cool130App?

Things can get out of hand

Typeclasses to the rescue

We have some animals

Typeclasses to the rescue

We have some animals

case class Cow(name: String)
case class Dog(name: String)
case class Kitty(name: String)

Silly original author! What noise do they make?

Wait.. There's no parent class..

What do we do?

Typeclasses to the rescue

Lets define a trait for things that can make sounds

Typeclasses to the rescue

Lets define a trait for things that can make sounds

trait Says[A] {
  def talk(thing: A): String
}

Now, let's try it out

Typeclasses to the rescue

Lets define a trait for things that can make sounds

trait Says[A] {
  def talk(thing: A): String
}

Now, let's try it out

object CowSays extends Says[Cow] {
  def talk(thing: Cow) = thing.name + " say mooooo"
}

scala> val cow = Cow("jerry")
cow: Cow = Cow(jerry)

scala> CowSays.talk(cow)
res1: String = jerry say mooooo

Typeclasses to the rescue

Not super useful

Typeclasses to the rescue

Not super useful

object CowSays extends Says[Cow] {
  def talk(thing: Cow) = thing.name + " say mooooo"
}
object KittySays extends Says[Kitty] {
  def talk(thing: Kitty) = thing.name + " say meooww"
}

scala> val (cow, kitty) = (Cow("jerry"), Kitty("ranjit"))
cow: Cow = Cow(jerry)
kitty: Kitty = Kitty(ranjit)

scala> CowSays.talk(cow)
res1: String = jerry say mooooo

scala> KittySays.talk(kitty)
res1: String = ranjit say meooww

Typeclasses to the rescue

It would be nice to have a ONE method call, i.e.

scala> Animal.talk(cow)
res1: String = jerry say mooooo

scala> Animal.talk(kitty)
res1: String = ranjit say meooww

Typeclasses to the rescue

It would be nice to have a single method call

implicit object CowSays extends Says[Cow] {
  def talk(thing: Cow) = thing.name + " say mooooo"
}

implicit object KittySays extends Says[Kitty] {
  def talk(thing: Kitty) = thing.name + " say meooww"
}

object Animal {
  def talk[A](animal: A)(implicit says: Says[A]) =
    says.talk(animal)
}

Well that's better!

Typeclasses to the rescue

It would be nice to have a single method call

implicit object CowSays   extends Says[Cow] ...
implicit object KittySays extends Says[Kitty] ...

object Animal {
  def talk[A](animal: A)(implicit says: Says[A]) =
    says.talk(animal)
}

Well that's better!

scala> Animal.talk(cow)
res0: String = jerry say mooooo

Typeclasses with Tuples!

We can bootstrap more complex datatypes

For example: We have a format for Cows, we can auto-generate one for (Cow, Cow)

Typeclasses with Tuples!

We can bootstrap more complex datatypes
For example: We have a format for Cows, we can auto-generate one for (Cow, Cow)

implicit def saysTuple[A, B]
    (implicit saysA: Says[A], saysB: Says[B])
  = new Says[(A, B)] {
    def talk(thing: (A, B)) =
      saysA.talk(thing._1) + " and " + saysB.talk(thing._2)
}

This says:

We have a Says[A]

We have a Says[B]

We can construct a Says[(A, B)] by having A talk, then B talk, then concatenating with "and"

Typeclasses with Tuples!

Now we can make tuples of Animals talk!

Typeclasses with Tuples!

Now we can make tuples of Animals talk!

scala> Animal.talk((cow, kitty))
res0: String = jerry say mooooo and ranjit say meooww

But that instance was ugly!

Typeclasses with Tuples, Pretty Version

We go from:

Typeclasses with Tuples, Pretty Version

We go from:

implicit def saysTuple[A, B]
    (implicit saysA: Says[A], saysB: Says[B])
  = new Says[(A, B)] {
    def talk(thing: (A, B)) =
      saysA.talk(thing._1) + " and " + saysB.talk(thing._2)
}

To:

Typeclasses with Tuples, Pretty Version

We go from:

implicit def saysTuple[A, B]
    (implicit saysA: Says[A], saysB: Says[B])
  = new Says[(A, B)] {
    def talk(thing: (A, B)) =
      saysA.talk(thing._1) + " and " + saysB.talk(thing._2)
}

implicit def saysTuple[A : Says, B : Says]
  = new Says[(A, B)] {
    def talk(thing: (A, B)) =
      Animal.talk(thing._1) + " and " + Animal.talk(thing._2)
}

"A : Says" asks the compiler to look for an implicit Says[A]

Typeclasses with Lists, Pretty Version

Or for lists

implicit def saysTuple[A : Says]
  = new Says[List[A]] {
    def talk(things: List[A]) =
      things.map(Animal.talk(_)).mkString(", ")
    }

"A : Says" asks the compiler to look for an implicit Says[A]

Typeclasses

Important in HW6, remember this pattern

Your JSON serialization will look very similar to this

COURSE WRAP-UP

Course Wrap-Up

We have studied many general themes in the context of

(the core of) OCaml and
(a sliver of) Scala

Theme: Expressions, Values, Types

Expressions and Values

Expressions are the programs that can be written in a language.

At run-time, expressions evaluate either

to a finished value

to a run-time error

or infinitely loop.

The semantics of evaluation can be defined

without any notion of types (e.g. OCaml or NanoML)

with a notion of types (e.g. instanceOf in Scala or Java)

Theme: Expressions, Values, Types

Types

Types are a compile-time description of run-time behavior.

Rule out certain classes of errors...

But not all. (e.g. null pointers, infinite loops)

Preventing larger classes of errors is active research area.

Theme: First-Class Functions

Functions are data!

They can be returned from functions.

They can be passed to (higher-order) functions as parameters.

Facilitate reusable, generic programming patterns.

Theme: Immutable vs. Mutable Data

Easier to understand, debug, and change programs when data cannot be mutated all over the place.

Mutation is often helpful or necessary, but use it with discretion.

Immutable Data taking over the world ...

Theme: Type Inference

Do not have to write types everywhere to get benefits of static types.

Global type inference in OCaml.

Local type inference in Scala.

Verbosity of Java/C# is a bad argument against static types ...!

Static Types taking over the world ...

Course Wrap-Up

Remember these powerful building blocks when you:

Learn new languages (Python, JavaScript, Erlang, Haskell, Go, Rust, ...).

Choose which languages to write your own code.

Choose how you write code in whatever language you are using.

Design your own programming languages!

</CSE 130>

Digression

Digression: Cons

How does cons work?

scala> 1 :: 2 :: 3 :: Nil
res27: List[Int] = List(1, 2, 3)

No big surprise... :: is a method!

What is the above expression equivalent to?

Is it 1.::(2.::(3.::(Nil))) ?

Fixity of Operators

Methods that end in : (like cons ) are associated from right-to-left.

scala> 1.::(2.::(3.::(Nil)))
res33: List[Double] = List(1.0, 2.0, 3.0)

scala> Nil.::(3.).::(2.).::(1.)
res2: List[Double] = List(1.0, 2.0, 3.0)

scala> Nil.::(3).::(2).::(1)
res0: List[Int] = List(1, 2, 3)

Announcements

Course Evaluations

CAPE

Topics

Final Exam

Practice Questions

Review Session

A Tale of Two Polymorphisms

Today's Plan

Parametric Polymorphism ("Type Variables"; ML style)

Combining Subtyping + Parametric Polymorphism

Proxies and Implicits

Functions with Type Variables

Parametrically Polymorphic Functions

Parametrically Polymorphic Functions

Parametrically Polymorphic Lists

Parametrically Polymorphic Lists

Parametrically Polymorphic Lists

Remember OCaml Datatypes?

Remember OCaml Datatypes?

Datatypes vs. Classes

OCaml Datatypes

Scala Classes

Case Classes

CLICKER: Case Classes

Case Classes

CLICKER: Case Classes

Case Classes

Sealed Classes

Parametric Polymorphism: List Length

Parametric Polymorphism: List Map

Are These Functions Equivalent?

Are These Functions Equivalent?

Are These Functions Equivalent?

Classes/Traits with Type Variables

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Parametrically Polymorphic Classes

Today's Plan

Parametric Polymorphism ("Type Variables"; ML style)

Combining Subtyping + Parametric Polymorphism

Proxies and Implicits

Combining Subtyping + Parametric Polymorphism

CLICKER: What is the value of res?

What is the value of res?

Want to describe WHICH types support comparison...

Traits!

An Ordered List...

An Ordered List... with Bounded Quantification

Bag is a pretty lame data structure

An Ordered Bag

An Ordered Bag

An Ordered Bag

An Ordered Bag

RECAP: Bounded Quantification

CLICKER: What is the value of res?

What is the value of res?

What is the value of res?

How to Add Functionality to Existing Types?

Today's Plan

Parametric Polymorphism ("Type Variables"; ML style)

Combining Subtyping + Parametric Polymorphism

Proxies and Implicits

Retrofitting Functionality with Proxies

Retrofitting Functionality with Proxies

Retrofitting Functionality with Proxies

Retrofitting Functionality with Proxies

Retrofitting Functionality with Proxies

Proxies are Awesome

... But Proxies are Also Lame

Let's Keep the Awesome and Eliminate the Lame

Implicit Parameters and Values

Implicit Parameters and Values

Implicits: The Magic of Types

Implicits: Automatically "Fix" Type Errors

Combining Subtyping
+ Parametric Polymorphism

CLICKER: What is the value of `res`?

What is the value of `res`?

Want to describe WHICH types
support comparison...

`Bag` is a pretty lame data structure

An Ordered `Bag`

CLICKER: What is the value of `res`?

What is the value of `res`?

What is the value of `res`?

Let's Keep the Awesome and
Eliminate the Lame